题目内容
17.双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1的左焦点到右顶点的距离为( )| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
分析 求得双曲线的a,b,由c=$\sqrt{{a}^{2}+{b}^{2}}$,可得c,即可得到左焦点和右顶点,进而得到它们的距离.
解答 解:双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1的a=2,b=$\sqrt{5}$,
c=$\sqrt{4+5}$=3,
可得右顶点为(2,0),左焦点为(-3,0),
可得左焦点到右顶点的距离为5.
故选:D.
点评 本题考查双曲线的左焦点和右顶点的距离,注意运用双曲线方程求得基本量a,b,c,考查运算能力,属于基础题.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x-1,x<0}\\{-{e}^{x}-x,x≥0}\end{array}\right.$若关于x的方程f(x)+m=0有3个实数根,则实数m的取值范围为( )
| A. | (1,3) | B. | (-3,-1) | C. | (1,5) | D. | (-5,-1) |
5.若f(x)=x+$\frac{4}{x}$,则下列结论正确的是( )
| A. | f(x)的最小值为4 | |
| B. | f(x)在(0,2)上单调递减,在(2,+∞)上单调递增 | |
| C. | f(x)的最大值为4 | |
| D. | f(x)在(0,2)上单调递增,在(2,+∞)上单调递减 |
12.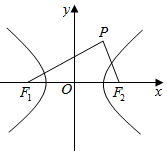 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{1}{2}$x | B. | y=±$\frac{\sqrt{5}}{5}$x | C. | y=±$\frac{2\sqrt{5}}{5}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
6.已知抛物线y2=4x的焦点到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线的距离为$\frac{1}{2}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{5}+1$ |
 在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.
在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.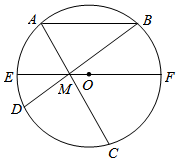 如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.
如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.