题目内容
已知函数f(x)＝2cos2
－
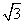sinx.
(1)求函数f(x)的最小正周期和值域；
(2)若α为第二象限角，且f(α－
)＝
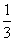，求
的值．
(1)因为f(x)＝1＋cosx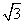－sinx＝1＋2cos(x＋)，
所以函数f(x)的最小正周期为2π，值域为[－1,3]．
(2)因为f(α－)＝，
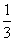所以1＋2cosα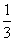＝，即cosα＝－.
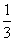又因为α为第二象限角，
所以sinα＝
.
练习册系列答案
相关题目
题目内容
已知函数f(x)＝2cos2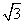－sinx.
(1)求函数f(x)的最小正周期和值域；
(2)若α为第二象限角，且f(α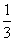－)＝，求的值．
(1)因为f(x)＝1＋cosx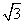－sinx＝1＋2cos(x＋)，
所以函数f(x)的最小正周期为2π，值域为[－1,3]．
(2)因为f(α－)＝，
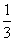所以1＋2cosα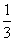＝，即cosα＝－.
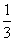又因为α为第二象限角，
所以sinα＝.
)．
，若f(
)＝2cos2α，求α的大小．
等于________．
＋
＝1上，则
的值为________．
，则
＝( )
B.
D．4
，则λ＝( )
B.