题目内容
已知函数f(x)=tan(2x+ ).
).
(1)求f(x)的定义域与最小正周期;
(2)设α∈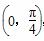 ,若f(
,若f(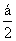 )=2cos2α,求α的大小.
)=2cos2α,求α的大小.
(1)由 ,k∈Z,得x≠
,k∈Z,得x≠ ,k∈Z,所以f(x)的定义域为
,k∈Z,所以f(x)的定义域为
f(x)的最小正周期为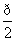 .
.
(2)由f =2cos2α得,
=2cos2α得,
tan =2cos2α,
=2cos2α, =2(cos2α-sin2α),
=2(cos2α-sin2α),
整理得 =2(cosα+sinα)(cosα-sinα).
=2(cosα+sinα)(cosα-sinα).
因为α∈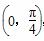 ,所以sinα+cosα≠0.
,所以sinα+cosα≠0.
因此(cosα-sinα)2= ,即sin2α=
,即sin2α= .
.
由α∈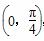 ,得2α∈
,得2α∈ .
.
所以2α= ,即α=
,即α= .
.

练习册系列答案
相关题目
 ,π),cos2x=a,则cosx=( )
,π),cos2x=a,则cosx=( )
 ),cos(α-
),cos(α- )=
)=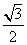 ,sin(
,sin( =________.
=________. -
-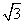 sinx.
sinx. )=
)=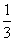 ,求
,求 的值.
的值.
 的值;
的值; |=( )
|=( )