题目内容
某城市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,但不超过40小时.设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).
(1)求f(x)和g(x);
(2)问:小张选择哪家比较合算?为什么?
[解析] (1)f(x)=5x(15≤x≤40);
g(x)=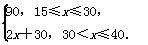
(2)由f(x)=g(x),得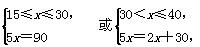
即x=18或x=10(舍).
当15≤x<18时,f(x)-g(x)=5x-90<0,
即f(x)<g(x),应选甲家;
当x=18时,f(x)=g(x),即可以选甲家也可以选乙家.
当18<x≤30时,f(x)-g(x)=5x-90>0,
即f(x)>g(x),应选乙家.
当30<x≤40时,
f(x)-g(x)=5x-(2x+30)=3x-30>0,
即f(x)>g(x),应选乙家.
综上所述:当15≤x<18时,选甲家;
当x=18时,可以选甲家也可以选乙家;
当18<x≤40时,选乙家.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
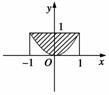
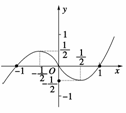
 的定义域为( )
的定义域为( ) +lg
+lg 的值是________.
的值是________. -
-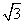 sinx.
sinx. )=
)=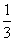 ,求
,求 的值.
的值.