题目内容
已知向量
=（2，1），
•
=10，|
+
|=5
，则|
|=（ ）
| a |
| a |
| b |
| a |
| b |
| 2 |
| b |
| A、5 | ||
| B、25 | ||
C、
| ||
D、
|
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据平面向量的数量积的运算，结合题意，求出
的模长．
| b |
解答：
解：∵向量
=（2，1），
•
=10，|
+
|=5
，
∴|
|=
=
，
∴(|
+
|)2=
2+2
•
+
2=(
)2+2×10+|
|2=(5
)2；
解得|
|2=25，
∴|
|=5．
故选：A．
| a |
| a |
| b |
| a |
| b |
| 2 |
∴|
| a |
| 22+12 |
| 5 |
∴(|
| a |
| b |
| a |
| a |
| b |
| b |
| 5 |
| b |
| 2 |
解得|
| b |
∴|
| b |
故选：A．
点评：本题考查了平面向量的应用问题，解题时应根据平面向量的数量积，求向量的模长，是基础题．
练习册系列答案
相关题目
椭圆与双曲线
-
=1有相同的焦点且离心率为
，则椭圆的标准方程为（ ）
| x2 |
| 3 |
| y2 |
| 2 |
| 1 | ||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线3x-2y-6=0在x轴上的截距为a，在y轴上的截距为b，则（ ）
| A、a=2，b=3 |
| B、a=-2，b=-3 |
| C、a=-2，b=3 |
| D、a=2，b=-3 |
函数f（x）=4sin（ωx-
）sin（ωx+
）（ω＞0）的最小正周期为π，且sinα=
，则f（α）=（ ）
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
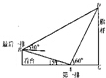某中学举行升旗仪式，如图所示，在坡度为15°的看台上，从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离AB=10执行如图所示的程序框图后，输出的值为4，则P的取值范围是（ ）
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
设i为虚数单位，则复数z=i2+i的实部和虚部分别是（ ）
| A、-1，i | B、-1，1 |
| C、1，i | D、1，1 |