题目内容
15.某篮球运动员在上赛季的三分球命中率为25%,场均三分球出手10次,教练建议他在新赛季减少三分球出手次数,若在新赛季的第一场比赛中该球员计划出手3次,每次出手均相互独立,设其命中X次.(1)若将频率视为概率,求X的分布列;
(2)请给该队员一些建议,如何才能提高他在一场比赛中的三分球得分的期望?
分析 (1)设X可以取0,1,2,3.求出概率,得到分布列.
(2)该队员应减少三分出手次数,以提高(3分)得分期望,当出手次数1个增加时,导致总得分期望会持续降低.
解答 (1)解:设X可以取0,1,2,3.
P(X=0)=${C}_{3}^{0}(\frac{3}{4})^{3}$=$\frac{27}{64}$,
P(X=1)=${C}_{3}^{1}(\frac{1}{4})(\frac{3}{4})^{2}$=$\frac{27}{64}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{4})^{2}•\frac{3}{4}$=$\frac{9}{64}$
P(X=3)=${C}_{3}^{3}(\frac{1}{4})^{3}(\frac{3}{4})^{0}$$\frac{1}{64}$
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
通过球员(3分)命中率以及得分期望来看,球员命中率为0.25,当出手次数1个增加时,其命中零次的概率需要乘以0.75,而与得分乘以零,导致总得分期望会持续降低.
点评 本题考查概率分布列,期望的求法,考查分析能力以及计算能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
20.已知(x+1)15=a0+a1x+a2x2+…+a15x15,则a0+a1+a2+…+a7=( )
| A. | 215 | B. | 214 | C. | 28 | D. | 27 |
7.若离散型随机变量X的分布列函数为P(X=k)=$\frac{k}{10}$,k=1,2,3,4,则P(X>1)=( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
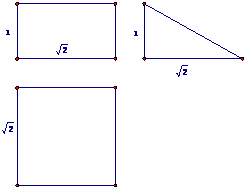 若某空间几何体的三视图如图所示.
若某空间几何体的三视图如图所示.