题目内容
函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f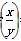 =f(x)-f(y),当x>1时,有f(x)>0.
=f(x)-f(y),当x>1时,有f(x)>0.
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
解:(1)∵当x>0,y>0时,f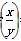 =f(x)-f(y),
=f(x)-f(y),
∴令x=y>0,则f(1)=f(x)-f(x)=0.
(2)设x1,x2∈(0,+∞),且x1<x2,
则f(x2)-f(x1)=f ,
,
∵x2>x1>0,∴ >1,∴f
>1,∴f >0.
>0.
∴f(x2)>f(x1),即f(x)在(0,+∞)上是增函数.
(3)由(2)知f(x)在[1,16]上是增函数.
∴f(x)min=f(1)=0,f(x)max=f(16),
∵f(4)=2,由f =f(x)-f(y),
=f(x)-f(y),
知f =f(16)-f(4),
=f(16)-f(4),
∴f(16)=2f(4)=4,
∴f(x)在[1,16]上的值域为[0,4].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的焦点的直线
的焦点的直线 与抛物线交于A.B两点,且△OAB(O为坐标原点)的面积为
与抛物线交于A.B两点,且△OAB(O为坐标原点)的面积为 ,则
,则 = .
= . ∈R,2
∈R,2 =5,则
=5,则 p为
p为 R,2
R,2 R,2
R,2 5
5 ∈R,2
∈R,2 =5 (D)
=5 (D) B.y=e-x
B.y=e-x
 C.6
C.6 β ②α⊥γ,β∥γ⇒α⊥β ③l∥α,l⊥β⇒α⊥β.
β ②α⊥γ,β∥γ⇒α⊥β ③l∥α,l⊥β⇒α⊥β.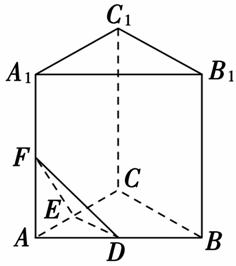
 的图象重合的函数是( )
的图象重合的函数是( ) B.f(x)=
B.f(x)=
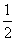 x-1 D.f(x)=
x-1 D.f(x)=