题目内容
一个球与一个正三棱柱的三个侧面和两个底面均相切,已知球的体积是 π,那么这个三棱柱的体积是( )
π,那么这个三棱柱的体积是( )
 π,那么这个三棱柱的体积是( )
π,那么这个三棱柱的体积是( )A.96 | B.16 | C.24 | D.48 |
D
解:由球的体积公式,得 πR3=
πR3= ∴R=2.∴正三棱柱的高h=2R=4。设正三棱柱的底面边长为a,则其内切圆的半径为
∴R=2.∴正三棱柱的高h=2R=4。设正三棱柱的底面边长为a,则其内切圆的半径为 =2,∴a=4
=2,∴a=4 ∴该正三棱柱的体积为
∴该正三棱柱的体积为
V=S底•h= •a•a•sin60°•h=
•a•a•sin60°•h= •(4
•(4 )2•4=48
)2•4=48
故答案为D
 πR3=
πR3= ∴R=2.∴正三棱柱的高h=2R=4。设正三棱柱的底面边长为a,则其内切圆的半径为
∴R=2.∴正三棱柱的高h=2R=4。设正三棱柱的底面边长为a,则其内切圆的半径为 =2,∴a=4
=2,∴a=4 ∴该正三棱柱的体积为
∴该正三棱柱的体积为V=S底•h=
 •a•a•sin60°•h=
•a•a•sin60°•h= •(4
•(4 )2•4=48
)2•4=48
故答案为D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
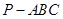 中,
中,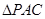 和
和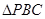 是边长为
是边长为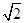 的等边三角形,
的等边三角形,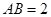 ,
,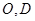 分别是
分别是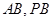 的中点.
的中点.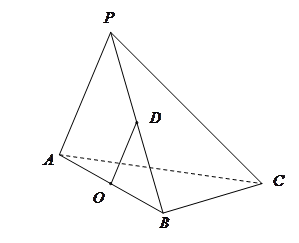
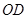 ∥平面
∥平面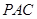 ;
;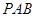 ⊥平面
⊥平面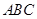 ;
; 满足
满足 ,若
,若 的最大值为
的最大值为 ,最小值为
,最小值为 ,则a的范围为 ( )
,则a的范围为 ( )






 π
π π
π  π
π π
π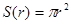 ,周长
,周长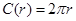 ,若将
,若将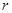 看作是
看作是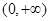 上的变量,则
上的变量,则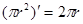 ……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为
……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为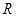 的球,若将
的球,若将