题目内容
质监部门对一批产品进行质检,已知样品中有合格品7件,次品3件.
(Ⅰ)若对样品进行逐个检测,求连续检测到三件次品的概率;
(Ⅱ)若从样品中一次抽取3件产品进行检测,求检测到次品数X的分布列及数学期望.
(Ⅰ)若对样品进行逐个检测,求连续检测到三件次品的概率;
(Ⅱ)若从样品中一次抽取3件产品进行检测,求检测到次品数X的分布列及数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:应用题,概率与统计
分析:(Ⅰ)确定所有基本事件总数,连续检测到三件次品基本事件总数,即可求连续检测到三件次品的概率;
(Ⅱ)取出的3件产品中次品的件数X可能为0,1,2,3,求出相应的概率,从而可得概率分布列与期望.
(Ⅱ)取出的3件产品中次品的件数X可能为0,1,2,3,求出相应的概率,从而可得概率分布列与期望.
解答:
解:(Ⅰ)合格品7件,次品3件,对样品进行逐个检测,共有基本事件
种,其中连续检测到三件次品,共有8种,
∴连续检测到三件次品的概率
=
;
(Ⅱ)依题意知,X可取0,1,2,3,则
∴P(X=0)=
,P(X=1)=
,
P(X=2)=
,P(X=3)=
.
X的分布列为:
∴EX=0×
+1×
+2×
+3×
=
.
| A | 3 10 |
∴连续检测到三件次品的概率
8
| ||
|
| 1 |
| 15 |
(Ⅱ)依题意知,X可取0,1,2,3,则
∴P(X=0)=
| ||||
|
| ||||
|
P(X=2)=
| ||||
|
| ||
|
X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||||||||||||||||||||||||
| P |
|
|
|
|
| ||||
|
| ||||
|
| ||||
|
| ||
|
| 9 |
| 10 |
点评:本题以实际问题为载体,考查等可能事件的概率,考查随机变量的期望与分布列,难度不大.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
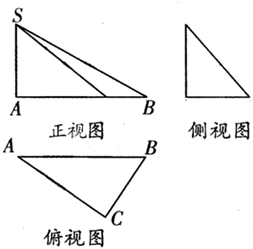 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
设i是虚数单位,则复数z=(
)2013=( )
| 1+i |
| 1-i |
| A、-1 | B、1 | C、-i | D、i |
为了了解小学生的作业负担,三名调研员对某校三年级1至5班进行学情调查,已知这5个班在同一层楼并按班号排列.若要求每名调研员均参与调查,但不在相邻两个班调查,每个班只安排一名调研员,则不同的调查方案有( )
| A、48种 | B、42种 |
| C、36种 | D、24种 |
命题:“?x∈R,2sinx≥1”的否定是( )
| A、?x∈R,2sinx<1 |
| B、?x∈R,2sinx≥1 |
| C、?x∈R,2sinx≤1 |
| D、?x∈R,2sinx<1 |