题目内容
在△ABC中，a，b，c分别为角A，B，C所对的边，a=2
，b=2，c=2
，求△ABC的面积S．
| 7 |
| 3 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：利用余弦定理表示出cosB，将三边长代入求出cosB的值，再利用同角三角函数间基本关系求出sinB的值，利用三角形面积公式即可求出三角形ABC面积．
解答：
解：∵a=2
，b=2，c=2
，
∴cosB=
=
=
，
∴sinB=
=
，
则S△ABC=
acsinB=2
×
=
．
| 7 |
| 3 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| 28+12-4 | ||
8
|
3
| ||
| 14 |
∴sinB=
| 1-cos2B |
| ||
| 14 |
则S△ABC=
| 1 |
| 2 |
| 21 |
| ||
| 14 |
| 3 |
点评：此题考查了余弦定理，同角三角函数间的基本关系，以及三角形的面积公式，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
设函数f（x）在R上存在导数f′（x），对任意的x∈R，有f（-x）+f（x）=x2，且x∈（0，+∞）时，f′（x）＞x．若f（2-a）-f（a）≥2-2a，则实数a的取值范围为（ ）
| A、[1，+∞） |
| B、（-∞，1] |
| C、（-∞，2] |
| D、[2，+∞） |
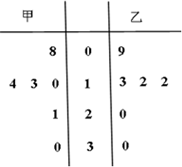在如图所示的茎叶图中，甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
. |
| S甲 |
. |
| S乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|