题目内容
已知椭圆C1: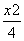 +
+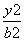 =1(0<b<2)的离心率为
=1(0<b<2)的离心率为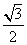 ,抛物线C2:x2=2py(p>0)的焦点是椭圆的顶点.
,抛物线C2:x2=2py(p>0)的焦点是椭圆的顶点.
(1)求抛物线C2的方程;
(2)过点M(-1,0)的直线l与抛物线C2交于E,F两点,过E,F作抛物线C2的切线l1,l2,当l1⊥l2时,求直线l的方程.
解:(1)∵椭圆C1的长半轴长a=2,半焦距c=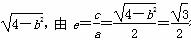 得b2=1,
得b2=1,
∴椭圆C1的上顶 点为(
点为( 0,1),
0,1),
∴抛物线C2的焦点为(0,1),
∴抛物线C2的方程为x2=4y.
(2)由已知可得直线l的斜率必存在,设直线l的方程为
y=k(x+1),E(x1,y1),F(x2,y2).由x2=4y得y= x2,
x2,
∴y′= x.
x.
∴切线l1,l2的斜率分别为 x1,
x1, x2.
x2.
当l1⊥l2时, x1·
x1· x2=-1,即x1x2=-4.
x2=-1,即x1x2=-4.
由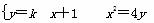 ,得x2-4kx-4k=0,
,得x2-4kx-4k=0,
∴Δ=(-4k)2-4×(-4k)>0,解得k<-1或k>0.①
由x1x2=-4k=-4,得k=1,满足①式,
∴直线l的方程为x-y+1=0.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 B.20
B.20 B.
B.
 D.
D.
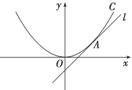
 片折叠使点A与点Q重合,然后展开纸片,折痕CD与OA交于点P,当点A运动时,点P的轨迹为( )
片折叠使点A与点Q重合,然后展开纸片,折痕CD与OA交于点P,当点A运动时,点P的轨迹为( ) ,则点P的轨迹为( )
,则点P的轨迹为( ) __.
__.