题目内容
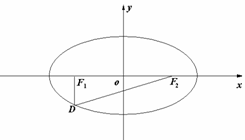
如图,设椭圆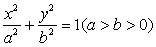 的左、右焦点分别为
的左、右焦点分别为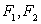 ,点
,点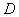 在椭圆上,
在椭圆上,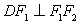 ,
,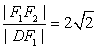 ,
,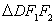 的面积为
的面积为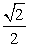 .
.
(1)求该椭圆的标准方程;
(2)是否存在圆心在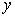 轴上的圆,使圆在
轴上的圆,使圆在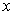 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
(1)设,其中,
由,得.
从而故.
从而,由得,因此.
所以,故.
因此,所求椭圆的标准方程为.

(2)如图,设圆心在轴上的圆与椭圆相交,是两个交点,,,是圆的切线,且由圆和椭圆的对称性,易知, ,
,
由(1)知,所以,
再由得,
由椭圆方程得,即,
解得或.
当时,重合,此时题设要求的圆不存在.
当时,过分别与,垂直的直线的交点即为圆心,设
由得而故.
圆的半径.
综上,存在满足条件的圆,其方程为.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
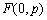 ,直线
,直线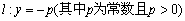 ,
,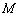 为平面内的动点,过
为平面内的动点,过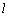 的垂线,垂足为
的垂线,垂足为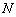 ,且
,且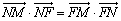 .
. 的方程;
的方程;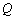 是
是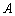 、
、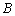 .
.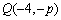 ,
,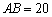 ,求
,求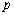 的值.
的值.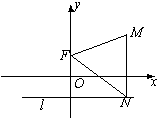
 平面上,点
平面上,点 ,点
,点 在单位圆上,
在单位圆上, (
( )
) ,求
,求 的值;
的值; ,
, ,求
,求 .
.
 的右准线为准线的抛物线方程是 .
的右准线为准线的抛物线方程是 . 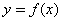 的两个极值点为
的两个极值点为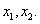 且
且 重合,
重合,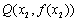 又在曲线
又在曲线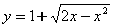 上,则曲线
上,则曲线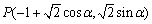 (其中
(其中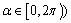 ,点
,点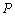 的轨迹记为曲线
的轨迹记为曲线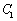 ,以坐标原点为极点,
,以坐标原点为极点,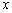 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点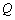 在曲线
在曲线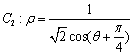 上.
上.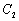 的直角坐标方程;
的直角坐标方程;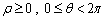 时,求曲线
时,求曲线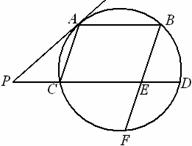
 的值域为
的值域为 ,若关于
,若关于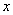 的不等式
的不等式 的解集为
的解集为 ,则实数
,则实数 的值为 .
的值为 .