题目内容
已知函数 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
.
(1)求 的表达式;
的表达式;
(2)若 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
(1)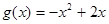 ;(2)
;(2)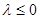 .
.
解析试题分析:(1)设函数的图象上任意一点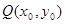 关于原点的对称点为
关于原点的对称点为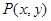 ,利用函数
,利用函数 和
和 的图象关于原点对称,可求得对称点之间的坐标关系,利用
的图象关于原点对称,可求得对称点之间的坐标关系,利用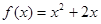 ,可求函数
,可求函数 的解析式;
的解析式;
(2)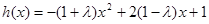 ,其对称轴方程为
,其对称轴方程为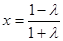 ,利用
,利用 在
在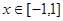 上是增函数,可求实数
上是增函数,可求实数 的取值范围.
的取值范围.
(1)设函数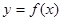 的图象上任意一点
的图象上任意一点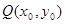 关于原点的对称点为
关于原点的对称点为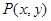 ,则
,则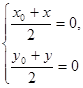 即
即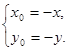 因为点
因为点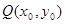 在函数
在函数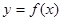 的图象上,所以
的图象上,所以 ,即
,即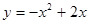 ,故
,故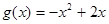 .
.
(2)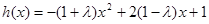
①当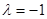 时,
时,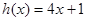 在
在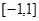 上是增函数,
上是增函数,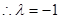
②当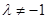 时,对称轴的方程为
时,对称轴的方程为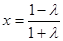 .
.
ⅰ)当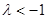 时,
时,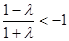 ,解得
,解得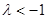 .
.
ⅱ)当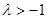 时,
时,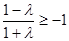 ,解得
,解得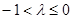 .
.
综上,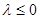 .
.
考点:二次函数的性质;函数的单调性;函数的对称性.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 在
在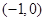 上是增函数.
上是增函数. 的取值范围
的取值范围 ;
; 满足:
满足: ,且
,且 ,
, ,并判断
,并判断 与
与 的大小.
的大小. 若存在
若存在 ,
, 成立,则称
成立,则称 为
为
 时,求函数
时,求函数 ,函数
,函数 的取值范围.
的取值范围.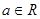 ,函数
,函数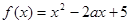 .
.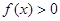 对任意
对任意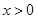 恒成立,求实数
恒成立,求实数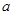 的最值范围;
的最值范围;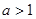 ,且函数
,且函数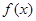 的定义域和值域均为
的定义域和值域均为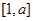 ,求实数
,求实数 其中
其中 且
且 .
.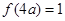 ,求
,求 的值;
的值; 上
上 恒成立,求
恒成立,求 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量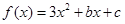 ,不等式
,不等式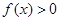 的解集为
的解集为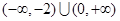 .
.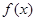 的解析式;
的解析式; 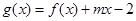 在
在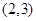 上单调,求实数
上单调,求实数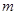 的取值范围;
的取值范围;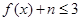 都成立,求实数n的最大值.
都成立,求实数n的最大值.