题目内容
7.已知sin($\frac{π}{3}$-α)=$\frac{1}{3}$,则sin($\frac{π}{6}$-2α)=( )| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $±\frac{7}{9}$ | D. | $-\frac{2}{9}$ |
分析 由已知利用诱导公式,二倍角的余弦函数公式即可计算得解.
解答 解:∵sin($\frac{π}{3}$-α)=cos[$\frac{π}{2}$-($\frac{π}{3}$-α)]=cos($\frac{π}{6}$+α)=$\frac{1}{3}$,
∴sin($\frac{π}{6}$-2α)=cos[$\frac{π}{2}$-($\frac{π}{6}$-2α)]=cos[2($\frac{π}{6}$+α)]=2cos2($\frac{π}{6}$+α)-1=2×$\frac{1}{9}$-1=-$\frac{7}{9}$.
故选:A.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
2.禽流感是家禽养殖业的最大威胁.为检验某新药物预防禽流感的效果,取80只家禽进行试验,得到如下丢失数据的列联表:(c,d,M,N表示丢失的数据)
(1)求出a,b,d,M,N的值,并判断:能否有99.5%的把握认为药物有效;
(2)若表中服用药后患病的5只家禽分别为3只鸡和2只鸭,现从这5只家禽中随机选取2只,求这2只家禽是同一类的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 患病 | 未患病 | 总计 | |
| 未服用药 | a | b | 40 |
| 服用药 | 5 | d | M |
| 总计 | 25 | N | 80 |
(2)若表中服用药后患病的5只家禽分别为3只鸡和2只鸭,现从这5只家禽中随机选取2只,求这2只家禽是同一类的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.已知(3-4i)$\overline{z}$=i101(其中$\overline z$为z的共轭复数,i为虚数单位),则复数z的虚部为( )
| A. | $\frac{3i}{25}$ | B. | -$\frac{3}{25}$ | C. | $\frac{3}{25}$ | D. | -$\frac{4}{25}$ |
16.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A作斜率为-1的直线l,该直线与双曲线的两条渐近线的交点分别为B,C,若$\overrightarrow{AB}=\frac{1}{2}\overrightarrow{BC}$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
17.已知函数f(x)=2sin(-2x+θ)(0<θ<π),$f({\frac{π}{4}})=-1$,则f(x)的一个单调递减区间是( )
| A. | $({-\frac{5π}{12},\frac{π}{12}})$ | B. | $({\frac{π}{12},\frac{7π}{12}})$ | C. | $({-\frac{π}{6},\frac{π}{3}})$ | D. | $({-\frac{π}{12},\frac{5π}{12}})$ |
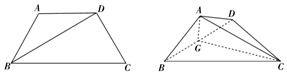 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.