题目内容
已知函数：
①f（x）=3lnx；
②f（x）=3ecosx；
③f（x）=3ex；
④f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
=3成立的函数是（ ）
①f（x）=3lnx；
②f（x）=3ecosx；
③f（x）=3ex；
④f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
| f(x1)f(x2) |
| A、③ | B、②③ | C、①②④ | D、④ |
考点：函数的值
专题：
分析：在①f（x）=3lnx中，f（1）=0，在④f（x）=3cosx中，f（0）=0，不存在自变量x2，使
=3成立；在②f（x）=3ecosx中，函数不是单调函数；在③f（x）=3ex中，函数是单调函数，且函数值不为0，由此能求出结果．
| f(x1)f(x2) |
解答：
解：在①f（x）=3lnx中，∵f（1）=0，∴不存在自变量x2，使
=3成立，故①不成立；
在②f（x）=3ecosx中，∵函数不是单调函数，
∴对于定义域内的任意一个自变量x1，使
=3成立的自变量x2不唯一，故②不成立；
在③f（x）=3ex中，函数是单调函数，且函数值不为0，
故定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
=3成立，故③成立；
在④f（x）=3cosx中，∵f（0）=0，∴不存在自变量x2，使
=3成立，故④不成立．
故选：A．
| f(x1)f(x2) |
在②f（x）=3ecosx中，∵函数不是单调函数，
∴对于定义域内的任意一个自变量x1，使
| f(x1)f(x2) |
在③f（x）=3ex中，函数是单调函数，且函数值不为0，
故定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
| f(x1)f(x2) |
在④f（x）=3cosx中，∵f（0）=0，∴不存在自变量x2，使
| f(x1)f(x2) |
故选：A．
点评：本题考查满足条件的函数的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
备战中考寒假系列答案
相关题目
若A={2，3，4}，B={x|x=m+n，m，n∈A，m≠n}，则集合B中的元素个数是（ ）
| A、2 | B、3 | C、4 | D、5 |
化简：tan（18°-x）tan（12°+x）+
[tan（18°-x）+tan（12°+x）]得（ ）
| 3 |
| A、0 | ||||
| B、1 | ||||
C、
| ||||
D、
|
函数f（x）=1-2sin2x的最小正周期是（ ）
| A、π | ||
| B、2π | ||
C、
| ||
| D、2 |
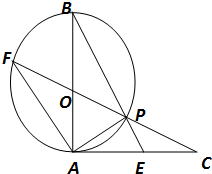已知：如图，AB是⊙O的直径，AC与⊙O相切于点A，且AC=AB，CO与⊙O相交于点P，CO的延长线与⊙O相交于点F，BP的延长线与AC相交于点E．