题目内容
在等差数列{an}中，a2+a7=20，则数列{an}的前8项之和S8= ．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质可得a1+a8=20，代入求和公式计算可得．
解答：
解：由等差数列的性质可得a1+a8=a2+a7=20，
∴数列{an}的前8项之和S8=
=80
故答案为：80
∴数列{an}的前8项之和S8=
| 8(a1+a8) |
| 2 |
故答案为：80
点评：本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
相关题目
函数f（x）=1-2sin2x的最小正周期是（ ）
| A、π | ||
| B、2π | ||
C、
| ||
| D、2 |
若-2i+1=a+bi，则a-b=（ ）
| A、-3 | B、-1 | C、1 | D、3 |
函数y=
的定义域为（ ）
log
|
A、（1，
| ||
B、[1，
| ||
| C、（1，2] | ||
| D、（1，2） |
若函数f（x）=
的定义域为（ ）
|
| A、[0，1） |
| B、（0，1） |
| C、（-∞，0]∪（1，+∞） |
| D、（-∞，0）∪（1，+∞） |
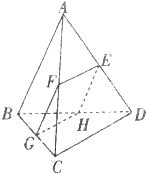如图，在四面体ABCD中，BC-AB，BD-AD截面EFGH平行于对棱AB和CD．