题目内容
已知函数f(x)=x3-2x+2有唯一零点,则存在零点的区间是( )
A、(-2,-
| ||
B、(-
| ||
C、(-1,-
| ||
D、(-
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数的解析式,结合零点存在定理,我们可以分别判断四个答案中的四区间,如果区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点.
解答:
解:已知函数f(x)=x3-2x+2有唯一零点,而且f(-2)=-8+4+2=-6<0,f(-
)=-
+5=
>0,
故存在零点的区间是 (-2,-
),
故选A.
| 3 |
| 2 |
| 27 |
| 8 |
| 13 |
| 8 |
故存在零点的区间是 (-2,-
| 3 |
| 2 |
故选A.
点评:本题考查的知识点是函数零点的判定定理,其中连续函数在区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点,是判断函数零点存在最常用的方法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知△ABC中,AB=4,BC=6,∠ABC=30°,一只蚂蚁在该三角形区域内随机爬行,则其恰好在离三个顶点距离都大于1的地方的概率为( )
A、
| ||
B、1-
| ||
C、1-
| ||
D、
|
某几何体的三视图如图所示,则该几何体的表面积为( )
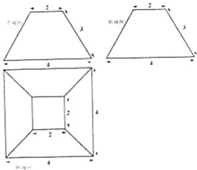

A、20+12
| ||
B、20+24
| ||
C、20+12
| ||
| D、56 |
 如图,过坐标原点O作倾斜角为60°的直线交抛物线Γ:y2=x于P1点,过P1点作倾斜角为120°的直线交x轴于Q1点,交Γ于P2点;过P2点作倾斜角为60°的直线交x轴于Q2点,交Γ于P3点;过P3点作倾斜角为120°的直线,交x轴于Q3点,交Γ于P4点;如此下去….又设线段OQ1,Q1Q2,Q2Q3,…,Qn-1Qn,…的长分别为a1,a2,a3,…,an,…,△OP1Q1,△Q1P2Q2,△Q2P3Q3,…,△Qn-1PnQn,…的面积分别为G1,G2,G3,…,Gn,…,数列{an}的前n项的和为Sn.
如图,过坐标原点O作倾斜角为60°的直线交抛物线Γ:y2=x于P1点,过P1点作倾斜角为120°的直线交x轴于Q1点,交Γ于P2点;过P2点作倾斜角为60°的直线交x轴于Q2点,交Γ于P3点;过P3点作倾斜角为120°的直线,交x轴于Q3点,交Γ于P4点;如此下去….又设线段OQ1,Q1Q2,Q2Q3,…,Qn-1Qn,…的长分别为a1,a2,a3,…,an,…,△OP1Q1,△Q1P2Q2,△Q2P3Q3,…,△Qn-1PnQn,…的面积分别为G1,G2,G3,…,Gn,…,数列{an}的前n项的和为Sn.