题目内容
设a,b,c均为正数,且a+b+c=12,则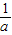 +
+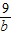 +
+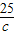 的最小值为 .
的最小值为 .
【答案】分析:利用条件a+b+c=12,构造柯西不等式(1+3+5)2≤(a+b+c)(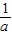 +
+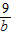 +
+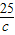 )进行解题即可.
)进行解题即可.
解答:解:由柯西不等式得(1+3+5)2≤(a+b+c)(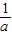 +
+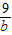 +
+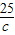 ),
),
∵a+b+c=12,
∴(1+3+5)2≤12(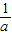 +
+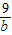 +
+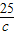 ),
),
∴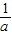 +
+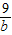 +
+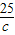 ≥
≥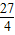 ,
,
当且仅当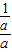 =
=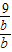 =
=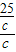 取等号,
取等号,
则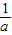 +
+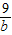 +
+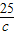 的最小值为
的最小值为 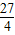 .
.
故答案为: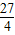 .
.
点评:本题主要考查了函数的值域,以及柯西不等式的应用,解题的关键是利用(1+3+5)2≤(a+b+c)(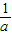 +
+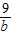 +
+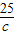 )进行解题,属于中档题.
)进行解题,属于中档题.
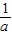 +
+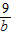 +
+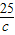 )进行解题即可.
)进行解题即可.解答:解:由柯西不等式得(1+3+5)2≤(a+b+c)(
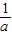 +
+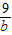 +
+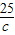 ),
),∵a+b+c=12,
∴(1+3+5)2≤12(
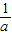 +
+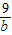 +
+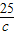 ),
),∴
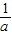 +
+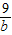 +
+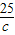 ≥
≥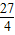 ,
,当且仅当
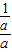 =
=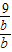 =
=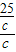 取等号,
取等号,则
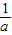 +
+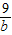 +
+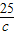 的最小值为
的最小值为 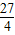 .
.故答案为:
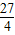 .
.点评:本题主要考查了函数的值域,以及柯西不等式的应用,解题的关键是利用(1+3+5)2≤(a+b+c)(
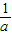 +
+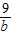 +
+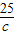 )进行解题,属于中档题.
)进行解题,属于中档题. 
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
设a,b,c均为正数,且2a=log
a,(
)b=log
b,(
)c=log2c,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |