题目内容
17.已知定义在R上偶函数f(x)满足f(x+2)•f(x)=4,且f(x)>0,则f(2017)=2.分析 根据题意,由f(x+2)•f(x)=4①可以构造f(x+4)•f(x+2)=4②,联立两个式子可得f(x+4)=f(x),即函数f(x)的周期为4;在f(x+2)•f(x)=4中令x=1可得f(1)f(-1)=4,结合函数为偶函数可得f(1)2=4,计算可得f(1)的值,由函数的周期性可得f(2017)=f(1+4×504)=f(1),即可得答案.
解答 解:根据题意,函数f(x)满足f(x+2)•f(x)=4,①
则有f(x+4)•f(x+2)=4,②
又由f(x)>0,联立①②可得:f(x+4)=f(x),即函数f(x)的周期为4,
在f(x+2)•f(x)=4中,令x=-1可得:f(1)f(-1)=4,
又由函数f(x)为偶函数,即f(-1)=f(1),
则有f(1)2=4,又由f(x)>0,则有f(1)=2,
则f(2017)=f(1+4×504)=f(1)=2;
即f(2017)=2;
故答案为:2.
点评 本题考查函数值的计算,涉及函数的奇偶性与周期性,关键是求出f(1)、f(-1)的值.

练习册系列答案
相关题目
5.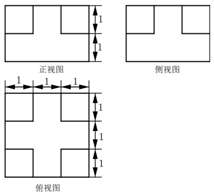 榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )
榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )
 榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )
榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
12.记复数z的共轭复数为$\overline z$,若$\overline z•({1-i})=2i$(i为虚数单位),则复数z在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |