题目内容
16.在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L距离”定义为:||P1P2||=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L距离”之和等于定值(大于||F1F2||)的点的轨迹可以是( )| A. |  | B. | 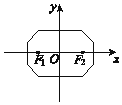 | C. | 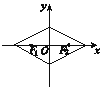 | D. | 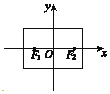 |
分析 根据题意,设出F1,F2的坐标,再设动点M的坐标,可得|x+c|+|x-c|+2|y|=m,分类讨论消去绝对值,化简方程,进而结合选项分析可得答案.
解答 解:设F1(-c,0),F2(c,0),
再设动点M(x,y),动点到定点F1,F2的“L-距离”之和等于m(m>2c>0),
由题意可得:|x+c|+|y|+|x-c|+|y|=m,即|x+c|+|x-c|+2|y|=m.
当x<-c,y≥0时,方程化为2x-2y+m=0;
当x<-c,y<0时,方程化为2x+2y+m=0;
当-c≤x<c,y≥0时,方程化为y=$\frac{m}{2}$-c;
当-c≤x<c,y<0时,方程化为y=c-$\frac{m}{2}$;
当x≥c,y≥0时,方程化为2x+2y-m=0;
当x≥c,y<0时,方程化为2x-2y-m=0.
结合题目中给出的四个选项可知,选项A中的图象符合要求.
故选:A.
点评 本题考查轨迹方程的求法,涉及分类讨论求解析式方程,解答的关键是正确分类讨论,求出每一种情况下的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在△ABC中,点E满足$\overrightarrow{BE}=3\overrightarrow{EC}$,且$\overrightarrow{AE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m-n=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
6.已知集合A={x|x≥2,或x≤-1},B={x|log3(2-x)≤1},则A∩(∁RB)=( )
| A. | {x|x<-1} | B. | {x|x≤-1,或x>2} | C. | {x|x≥2,或x=-1} | D. | {x|x<-1,或x≥2} |