题目内容
15.已知a>0,二项式($\sqrt{x}$+$\frac{2a}{x}$)6展开式中的常数项为240,则${∫}_{0}^{\frac{π}{a}}$sin(x-$\frac{π}{3}$)dx=$\frac{1-\sqrt{3}}{2}$.分析 运用二项式展开式的通项公式,化简整理,再令x的次数为0,求出a,再由定积分的运算法则,即可求得
解答 解:二项式($\sqrt{x}$+$\frac{2a}{x}$)6展开式的通项公式为:Tk+1=${C}_{6}^{k}(2a)^{k}{x}^{\frac{6-3k}{2}}$
令6-3k=0,则k=2.
即有C63•(2a)3=240,即a=2.
则${∫}_{0}^{\frac{π}{a}}$sin(x-$\frac{π}{3}$)dx=${∫}_{0}^{\frac{π}{2}}$(sin(x-$\frac{π}{3}$))dx=-cos(x-$\frac{π}{3}$)|${\;}_{0}^{\frac{π}{2}}$=-(cos$\frac{π}{6}$-cos$\frac{π}{3}$)=$\frac{1-\sqrt{3}}{2}$.
故答案为:$\frac{1-\sqrt{3}}{2}$.
点评 本题考查二项式定理的运用:求特定项,同时考查定积分的运算,属于基础题.

练习册系列答案
相关题目
3.已知向量|$\overrightarrow{a}$|=5,$\overrightarrow{b}$=(2,1)且$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ>0),则$\overrightarrow{a}$的坐标是( )
| A. | ($\sqrt{5}$,2$\sqrt{5}$) | B. | (2$\sqrt{5}$,$\sqrt{5}$) | C. | (-$\sqrt{5}$,-2$\sqrt{5}$) | D. | (-2$\sqrt{5}$,-$\sqrt{5}$) |
20.执行如图的算法语句,则输出S为( )


| A. | $\frac{2015}{2016}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{4030}{2016}$ | D. | $\frac{2016}{2017}$ |
7.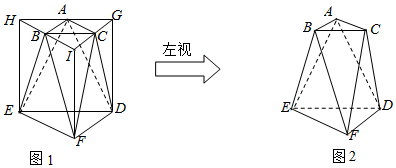 如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )
如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )
 如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )
如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )| A. |  | B. | 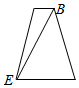 | C. | 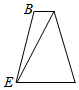 | D. | 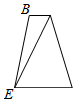 |
4.在△ABC中,已知sin(A-B)cosB+cos(A-B)sinB≥1,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
