题目内容
已知由样本数据点集{(xi,yi)|i=1,2,…,n}求得的回归直线方程为
=1.23x+0.08,且
=4.若去掉两个数据点(4.1,5.7)和(3.9,4.3)后重新求得的回归直线?的斜率估计值为1.2,则此回归直线?的方程为 .
| ∧ |
| y |
. |
| x |
考点:线性回归方程
专题:概率与统计
分析:由题意求出样本中心点,然后求解新的样本中心,利用回归直线?的斜率估计值为1.2,求解即可.
解答:
解:由样本数据点集{(xi,yi)|i=1,2,…,n}求得的回归直线方程为
=1.23x+0.08,且
=4.
=1.23×4+0.08=5,
去掉两个数据点(4.1,5.7)和(3.9,4.3),
=4.
=5,
重新求得的回归直线?的斜率估计值为1.2,回归直线方程设为:
=1.2x+a,代入(4,5),∴a=0.2
∴回归直线?的方程为:
=1.2x+0.2.
故答案为:
=1.2x+0.2
| ∧ |
| y |
. |
| x |
. |
| y |
去掉两个数据点(4.1,5.7)和(3.9,4.3),
. |
| x |
. |
| y |
重新求得的回归直线?的斜率估计值为1.2,回归直线方程设为:
| ∧ |
| y |
∴回归直线?的方程为:
| ∧ |
| y |
故答案为:
| ∧ |
| y |
点评:本题考查数据的回归直线方程,利用回归直线方程恒过样本中心点是关键.

练习册系列答案
相关题目
已知非零向量
,
满足|
-
|=|
+
|=λ|
|(λ≥2),则
-
与
+
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
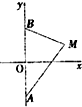 已知点A、B的坐标分别是(0,-1),(0,1),直线AM、BM相交于点M,且它们的斜率之积为-
已知点A、B的坐标分别是(0,-1),(0,1),直线AM、BM相交于点M,且它们的斜率之积为-