题目内容
5.函数f(x)=ex+ax-2,求f(x)的单调区间.分析 对f(x)求导,讨论a,得到不同的结论.
解答 解:∵f(x)=ex+ax-2
∴f′(x)=ex+a
①a≥0时,f′(x)>0恒成立,
∴f(x)在R上是单调递增的.
②a<0时,令f′(x)=0,得x=ln(-a)
∴f(x)在区间(-∞,ln(-a))上单调递减,在区间(ln(-a),+∞)上单调递增.
综上所述:a≥0时,f(x)在R上是单调递增的.
a<0时,f(x)在区间(-∞,ln(-a))上单调递减,在区间(-ln(-a),+∞)上单调递增.
点评 本题考查函数求导,及分论讨论.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 若命题p:?x∈R,x2-2x-1>0,则命题¬p:?x∈R,x2-2x-1<0 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “b2=ac”是“a,b,c成等比数列”的充要条件 |
20.下面如图是一个封闭几何体的三视图,则该几何体的体积为( )


| A. | π | B. | $\frac{5π}{3}$ | C. | $\frac{7π}{3}$ | D. | 3π |
14.已知a>0,x、y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$ 若z=2x+y的最小值与最大值的和为7,则a=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
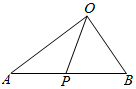 如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.
如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.