题目内容
13.一轮船要通过一座跨江大桥,驾驶员在A处测得桥拱上端D的仰角为8°,轮船向前航行200m后到B,又测得桥拱上端D的仰角为26°.若轮船驾驶舱离水面20m,轮船最高处距离驾驶舱上方有30m.问轮船能否通过这座跨江大桥?分析 作出示意图,利用正弦定理求出BD,再解直角三角形求出CD,与轮船驾驶舱上方高度比较得出结论.
解答  解由题意可知A=8°,∠DBC=26°,∴∠ADB=18°.
解由题意可知A=8°,∠DBC=26°,∴∠ADB=18°.
在△ABD中,由正弦定理得$\frac{200}{sin18°}=\frac{BD}{sin8°}$,
∴BD=$\frac{200sin8°}{sin18°}$≈90m.
∴CD=BDsin∠DBC=90sin26°≈39.5m.>30m.
答:轮船能通过这座跨江大桥.
点评 本题考查了解三角形的实际应用,属于基础题.

练习册系列答案
相关题目
3.对任意正数x,不等式x-2a>2-x恒成立,则a的取值范围为( )
| A. | $(-∞,-\frac{1}{2})$ | B. | $(-1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},0)$ | D. | $(-∞,-\frac{1}{2}]$ |
2.已知an=$\frac{n-\sqrt{2008}}{n-\sqrt{2009}}$,且数列{an}中共有100项,则此数列中最小项和最大项分别为第( )项.
| A. | 42,43 | B. | 43,44 | C. | 44,45 | D. | 45,46 |
3.在数列{an}中,an+1=can(c为非零常数),前n项和为Sn=3n-2+k,则实数k的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
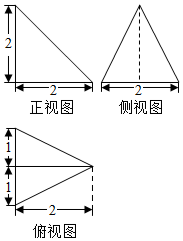 某三棱锥的三视图如图所示,则该三棱锥的表面积是4+2$\sqrt{6}$.
某三棱锥的三视图如图所示,则该三棱锥的表面积是4+2$\sqrt{6}$.