题目内容
17.已知直线l的法向量$\overrightarrow{n}$=(-3,2),并且与x轴、y轴围成的三角形的面积为3,求直线l的方程.分析 根据直线l的法向量写出l的方程,求出l与x轴、y轴的交点坐标,写出三角形的面积,从而求出直线l的方程.
解答 解:∵直线l的法向量为$\overrightarrow{n}$=(-3,2),
∴直线l的方程为-3x+2y+c=0,
∴直线l与x轴的交点为A($\frac{c}{3}$,0),与y轴的交点为B(0,-$\frac{c}{2}$);
∴△AOB的面积为$\frac{1}{2}$•|$\frac{c}{3}$|•|-$\frac{c}{2}$|=3,
解得c=±6;
∴直线l的方程为-3x+2y+6=0或-3x+2y-6=0,
即3x-2y-6=0或3x-2y+6=0.
点评 本题考查了直线的法向量以及直线与坐标轴的交点问题,也考查了三角形面积公式的应用问题,是基础题.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.空间四边形ABCD的两对边AB=CD=3,E、F分别是AD、BC上的点,且EF=$\sqrt{7}$,AE:ED=BF:FC=1:2,则AB与CD所成角大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
2.已知an=$\frac{n-\sqrt{2008}}{n-\sqrt{2009}}$,且数列{an}中共有100项,则此数列中最小项和最大项分别为第( )项.
| A. | 42,43 | B. | 43,44 | C. | 44,45 | D. | 45,46 |
9.设函数f(x)=x-2msinx+(2m-1)sinxcosx(m为实数)在(0,π)上为增函数,则m的取值范围为( )
| A. | [0,$\frac{2}{3}$] | B. | (0,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$] | D. | [0,$\frac{2}{3}$) |
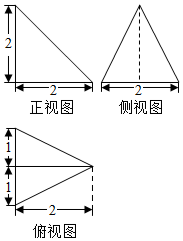 某三棱锥的三视图如图所示,则该三棱锥的表面积是4+2$\sqrt{6}$.
某三棱锥的三视图如图所示,则该三棱锥的表面积是4+2$\sqrt{6}$.