题目内容
二次函数f(x)满足f(x＋1)－f(x)＝2x，且f(0)＝1.
(1)求f(x)的解析式．
(2)在区间[－1,1]上，y＝f(x)的图象恒在y＝2x＋m的图象上方，试确定实数m的范围．
解 (1)设f(x)＝ax2＋bx＋c(a≠0)，由f(0)＝1，得c＝1，故f(x)＝ax2＋bx＋1.
因为f(x＋1)－f(x)＝2x，
所以a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x.
即2ax＋a＋b＝2x，所以
所以f(x)＝x2－x＋1.
(2)由题意得x2－x＋1>2x＋m在[－1,1]上恒成立，
即x2－3x＋1－m>0在[－1,1]上恒成立．
设g(x)＝x2－3x＋1－m，其图象的对称轴为直线x＝
，所以g(x)在[－1,1]上递减．
故只需g(1)>0，即12－3×1＋1－m>0，解得m<－1.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
则f
＝( )
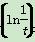<2f(1)时，那么t的取值范围是________．
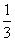≤a≤1，且f(x)在[1,3]上的最大值为M(a)，最小值为N(a)，令g(a)＝M(a)－N(a)，求g(a)的表达式．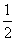
则方程f(x)＝
的解集为________．