题目内容
已知函数f(x)=ax2-2x+1.
(1)试讨论函数f(x)的单调性.
(2)若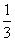 ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式.
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式.
(3)在(2)的条件下,求证:g(a)≥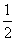
解 (1)当a=0时,函数f(x)=-2x+1在(-∞,+∞)上为减函数;
当a>0时,抛物线f(x)=ax2-2x+1开口向上,对称轴为x= ,
,
所以函数f(x)在 上为减函数,在
上为减函数,在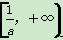 上为增函数;
上为增函数;
当a<0时,抛物线f(x)=ax2-2x+1开口向下,对称轴为x= ,
,
所以函数f(x)在 上为增函数,在
上为增函数,在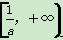 上为减函数.
上为减函数.
(2)因为f(x)=a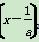 2+1-
2+1- ,
,
由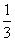 ≤a≤1得1≤
≤a≤1得1≤ ≤3,
≤3,
所以N(a)=f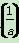 =1-
=1- .
.
当1≤ <2,即
<2,即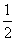 <a≤1时,M(a)=f(3)=9a-5,故g(a)=9a+
<a≤1时,M(a)=f(3)=9a-5,故g(a)=9a+ -6;
-6;
当2≤ ≤3,即
≤3,即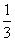 ≤a≤
≤a≤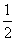 时,M(a)=f(1)=a-1,
时,M(a)=f(1)=a-1,
故g(a)=a+ -2.
-2.
所以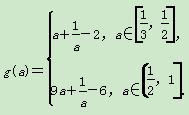
(3)证明:当a∈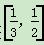 时,g′(a)=1-
时,g′(a)=1-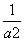 <0,
<0,
所以函数g(a)在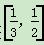 上为减函数;
上为减函数;
当a∈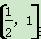 时,g′(a)=9-
时,g′(a)=9-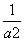 >0,
>0,
所以函数g(a)在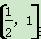 上为增函数,
上为增函数,
所以当a=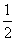 时,g(a)取最小值,
时,g(a)取最小值,
g(a)min=g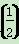 =
=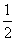 .
.
故g(a)≥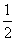 .
.

练习册系列答案
相关题目
 φ(x)=
φ(x)= 则当x<0时,f(φ(x))=________.
则当x<0时,f(φ(x))=________.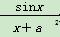 是奇函数,则a的值为( )
是奇函数,则a的值为( ) >2x B.2x>lgx>x
>2x B.2x>lgx>x B.xa>xb
B.xa>xb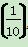 x在x∈[0,4]上解的个数是( )
x在x∈[0,4]上解的个数是( ) 是奇函数,且
是奇函数,且 ,则nm的取值范围为________.
,则nm的取值范围为________.