题目内容
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的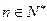 ,总有
,总有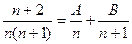 成立,求常数
成立,求常数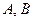 的值;
的值;
(2)在数列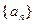 中,
中, ,
,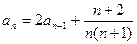 (
(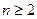 ,
,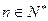 ),求通项
),求通项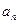 ;
;
(3)在(2)题的条件下,设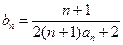 ,从数列
,从数列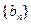 中依次取出第
中依次取出第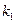 项,第
项,第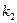 项,…第
项,…第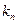 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列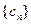 ,其中
,其中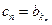 ,其中
,其中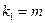 ,
,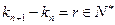 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数 的值;不存在,说明理由.
的值;不存在,说明理由.
题满分7分)
(1)若对于任意的
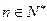 ,总有
,总有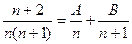 成立,求常数
成立,求常数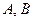 的值;
的值;(2)在数列
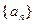 中,
中, ,
,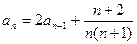 (
(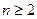 ,
,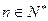 ),求通项
),求通项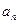 ;
;(3)在(2)题的条件下,设
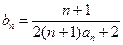 ,从数列
,从数列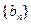 中依次取出第
中依次取出第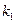 项,第
项,第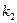 项,…第
项,…第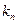 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列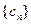 ,其中
,其中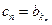 ,其中
,其中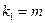 ,
,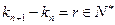 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数 的值;不存在,说明理由.
的值;不存在,说明理由.略
解:(1)由题设得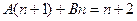 即
即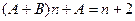 恒成立,
恒成立,
所以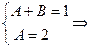
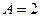 ,
,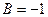 .…………………………………4分
.…………………………………4分
(2)由题设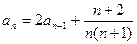 (
(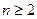 )又
)又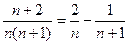 得,
得,
 ,且
,且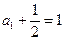 ,
,
即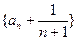 是首项为1,公比为2的等比数列,………………………………8分
是首项为1,公比为2的等比数列,………………………………8分
所以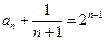 . 即
. 即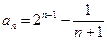 为所求.………………………………9分
为所求.………………………………9分
(3)假设存在正整数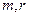 满足题设,由(2)知
满足题设,由(2)知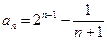
显然 ,又
,又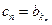 得
得 ,
,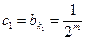
即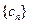 是以
是以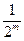 为首项,
为首项,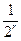 为公比的等比数列.………………11分
为公比的等比数列.………………11分
于是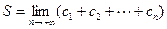
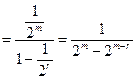 ,…………………12分
,…………………12分
由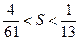 得
得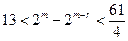 ,
,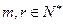 ,
,
所以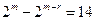 或
或 ,…………………………………………14分
,…………………………………………14分
 当
当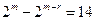 时,
时,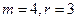 ;
;
当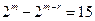 时,
时,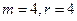 ;
;
综上,存在正整数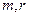 满足题设,
满足题设,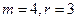 或
或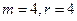 .……………16分
.……………16分
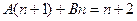 即
即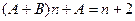 恒成立,
恒成立,所以
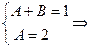
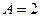 ,
,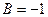 .…………………………………4分
.…………………………………4分(2)由题设
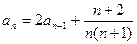 (
(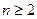 )又
)又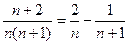 得,
得, ,且
,且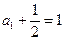 ,
,即
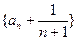 是首项为1,公比为2的等比数列,………………………………8分
是首项为1,公比为2的等比数列,………………………………8分所以
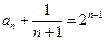 . 即
. 即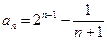 为所求.………………………………9分
为所求.………………………………9分(3)假设存在正整数
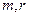 满足题设,由(2)知
满足题设,由(2)知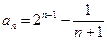
显然
 ,又
,又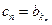 得
得 ,
,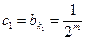
即
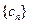 是以
是以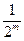 为首项,
为首项,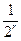 为公比的等比数列.………………11分
为公比的等比数列.………………11分于是
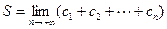
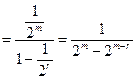 ,…………………12分
,…………………12分由
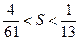 得
得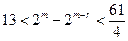 ,
,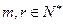 ,
,所以
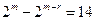 或
或 ,…………………………………………14分
,…………………………………………14分 当
当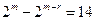 时,
时,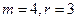 ;
;当
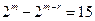 时,
时,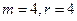 ;
; 综上,存在正整数
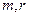 满足题设,
满足题设,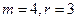 或
或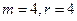 .……………16分
.……………16分
练习册系列答案
相关题目
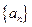 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,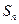 为
为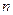 项和.
项和.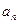 及
及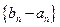 是首项为1,公比为3的等
是首项为1,公比为3的等 比数列,求数列
比数列,求数列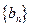 的通项公式及其前
的通项公式及其前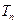 .
.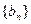 满足:
满足: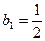 ,
,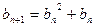 ,
, 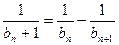 ;
;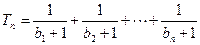 ,对任意的正整数
,对任意的正整数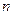 ,
,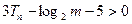 恒成立.求m的取值范围.
恒成立.求m的取值范围.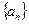 中,
中,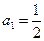 ,且当
,且当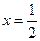 时,函数
时,函数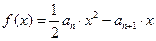 取得极值。
取得极值。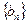 满足:
满足: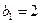 ,
,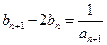 ,证明:
,证明: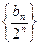 是等差数列,并求数列
是等差数列,并求数列 项及前
项及前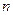 项和
项和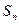 .
.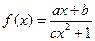 (
(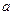 ,
,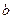 ,
,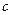 为常数,
为常数,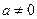 ).
).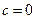 时,数列
时,数列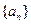 满足条件:点
满足条件:点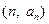 在函数
在函数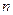 项和
项和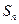 ;
;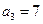 ,
,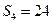 ,
,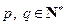 (
(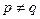 ),
),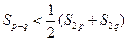 ;
;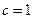 时,
时,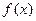 是奇函数,
是奇函数,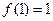 ,数列
,数列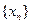 满足
满足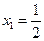 ,
,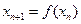 ,
,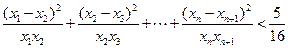 .
.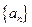 的前
的前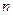 项和为
项和为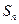 ,对
,对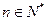 ,都有
,都有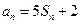 成立,
成立,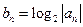 ,试
,试 求数列
求数列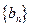 的前
的前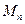
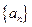 满足
满足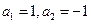 ,当
,当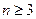 ,
,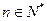 时,
时,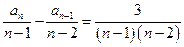 .
.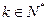 ,使得
,使得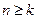 时,不等式
时,不等式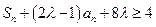 对任意实数
对任意实数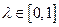 恒成立?若存在,求出
恒成立?若存在,求出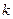 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.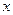 轴上是否存在定点
轴上是否存在定点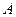 ,使得三点
,使得三点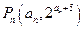 、
、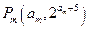 、
、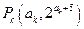 (其中
(其中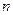 、
、 、
、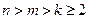 )到定点
)到定点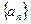 的前n项和为
的前n项和为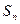 ,若
,若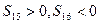 ,则
,则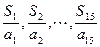 中最大的
中最大的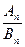 =
=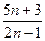 ,则
,则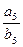 =
=