题目内容
(本小题满分16分)
已知数列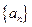 满足
满足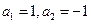 ,当
,当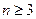 ,
,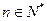 时,
时,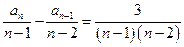 .
.
⑴求数列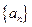 的通项公式;
的通项公式;
⑵是否存在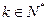 ,使得
,使得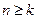 时,不等式
时,不等式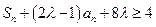 对任意实数
对任意实数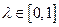 恒成立?若存在,求出
恒成立?若存在,求出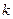 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
⑶在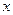 轴上是否存在定点
轴上是否存在定点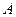 ,使得三点
,使得三点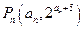 、
、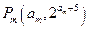 、
、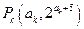 (其中
(其中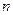 、
、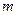 、
、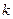 是互不相等的正整数且
是互不相等的正整数且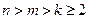 )到定点
)到定点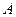 的距离相等?若存在,求出点
的距离相等?若存在,求出点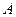 及正整数
及正整数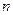 、
、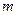 、
、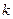 ;若不存在,说明理由.
;若不存在,说明理由.
已知数列
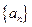 满足
满足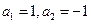 ,当
,当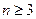 ,
,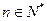 时,
时,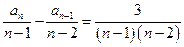 .
.⑴求数列
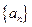 的通项公式;
的通项公式;⑵是否存在
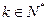 ,使得
,使得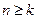 时,不等式
时,不等式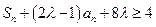 对任意实数
对任意实数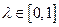 恒成立?若存在,求出
恒成立?若存在,求出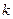 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.⑶在
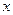 轴上是否存在定点
轴上是否存在定点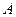 ,使得三点
,使得三点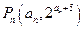 、
、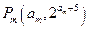 、
、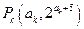 (其中
(其中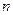 、
、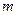 、
、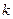 是互不相等的正整数且
是互不相等的正整数且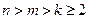 )到定点
)到定点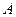 的距离相等?若存在,求出点
的距离相等?若存在,求出点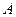 及正整数
及正整数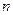 、
、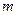 、
、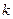 ;若不存在,说明理由.
;若不存在,说明理由.(1)

(2) 5
(3) 不存在
略

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
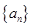 (
(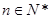 )的前n项和为
)的前n项和为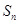 ,该数列是单调递增数列,若
,该数列是单调递增数列,若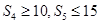 ,则
,则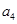 的取值范围是
的取值范围是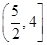
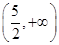
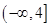
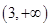
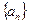 中,
中, ,且当
,且当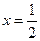 时,函数
时,函数
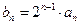 ,证明数列
,证明数列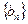 为等差数列;
为等差数列;
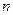 项和为
项和为 ,求
,求 
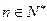 ,总有
,总有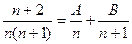 成立,求常数
成立,求常数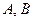 的值;
的值;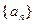 中,
中, ,
,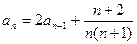 (
(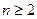 ,
,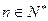 ),求通项
),求通项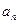 ;
;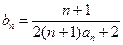 ,从数列
,从数列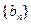 中依次取出第
中依次取出第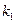 项,第
项,第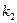 项,…第
项,…第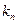 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列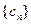 ,其中
,其中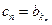 ,其中
,其中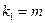 ,
,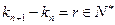 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 的前n项和为
的前n项和为 ,且
,且 , 则
, 则 等于
等于  }的前5项和
}的前5项和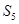 ="25," 且
="25," 且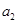 ="3," 则
="3," 则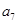 = ( )
= ( )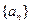 的前
的前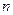 项和为
项和为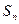 ,且
,且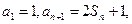 数列
数列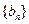 满足
满足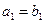 ,点
,点 在直线
在直线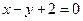 上,
上, .
. ,
,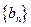 的通项公式;
的通项公式;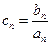 ,求数列
,求数列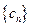 的前
的前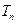 .
. 的前n项和记为
的前n项和记为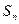 ,前
,前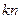 项和记为
项和记为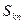
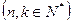 ,对给定的常数
,对给定的常数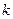 ,若
,若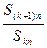 是与
是与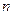 无关的非零常数
无关的非零常数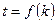 ,则称该数列
,则称该数列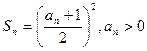 ,求数列
,求数列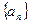 是一个 “
是一个 “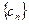 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比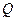
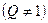 ,若数列
,若数列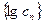 是一个 “
是一个 “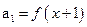 ,
,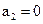 ,
,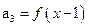 ,其中
,其中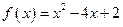 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。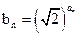 ,求数列
,求数列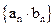 的前n项和
的前n项和