题目内容
10.(1)设0<x<$\frac{3}{2}$,求函数y=x(2-x)的最大值(2)已知x>3,求y=x+$\frac{4}{x-3}$的最小值.
分析 (1)由0<x<$\frac{3}{2}$,可得2-x>0,可得函数y=x(2-x)≤$(\frac{x+2-x}{2})^{2}$,即可得出.
(2)由x>3,可得x-3>0.可得y=x+$\frac{4}{x-3}$=x-3+$\frac{4}{x-3}$+3,利用基本不等式的性质即可得出.
解答 解:(1)∵0<x<$\frac{3}{2}$,∴2-x>0,
∴函数y=x(2-x)≤$(\frac{x+2-x}{2})^{2}$=1,当且仅当x=1时取等号.
当且仅当x=2-x时取等号,既x=1时,y的最大值为1,
(2)∵x>3,∴x-3>0.
∴y=x+$\frac{4}{x-3}$=x-3+$\frac{4}{x-3}$+3≥2$\sqrt{(x-3)•\frac{4}{x-3}}$+3=7.当且仅当x=5时取等号.
y的最小值为7.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.点M的直角坐标(2$\sqrt{3}$,-2)化成极坐标为( )
| A. | (4,$\frac{5π}{6}$) | B. | (4,$\frac{2π}{3}$) | C. | (4,$\frac{5π}{3}$) | D. | (4,$\frac{11π}{6}$) |
15.函数$f(x)=2sin(ωx+ϕ)(ω>0,-\frac{π}{2}<ϕ<\frac{π}{2})$的部分图象如图所示,则ω,ϕ的值为( )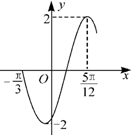

| A. | $2\;,\;\frac{2π}{3}$ | B. | $2\;,\;-\frac{π}{3}$ | C. | $1\;,\;\frac{π}{12}$ | D. | $1\;,\;-\frac{π}{12}$ |
2.△ABC,角A,B,C对应边分别为a,b,c,已知条件p:$\frac{a}{cosA}$=$\frac{b}{cosB}$,条件q:a=b,则p是q成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分也非必要条件 |