题目内容
19.关于直线m,n和平面α,β,有以下四个命题:①若m∥α,n∥β,α∥β,则m∥n;
②若m∥n,m?α,n⊥β,则α⊥β;
③若α∩β=m,m∥n,则n∥α且n∥β;
④若m⊥n,α∩β=m,则n⊥α或n⊥β.
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①m∥n或m,n相交或m,n异面;②由面面垂直的判定定理可得α⊥β;③n∥α或n?α,④n⊥α或n⊥β,但也有可能n与α,β斜交.
解答 解:①若m∥α,n∥β,α∥β,则m∥n或m,n相交或m,n异面,故①错误
②若m∥n,m?α,则
当n?α时,根据线面平行的判定定理可得n∥α,由n⊥β可得α⊥β,
当n?α时,由n⊥β,则可得m⊥β,由平面垂直的判定定理可得,α⊥β,故②正确
③若α∩β=m,m∥n,
当n⊆α时,满足已知;当n?α时,由线面平行的判定定理可得则n∥α
n与β的关系同理可判断,故③错误
④若m⊥n,α∩β=m,
若n⊆β,由线面垂直的判定定理可得则n⊥α或
若n⊆α,由线面垂直的判定定理可得n⊥β.
n?α,n?β时,n与α,β不垂直,即有可能n与α,β斜交,故④错误
故选A.
点评 本题主要题考查的知识点是平面的基本性质及推论,空间直线与平面位置关系的判断,其中根据面面平行,线面垂直的判定及性质,空间直线与平面位置关系的定义和几何特征.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
4.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )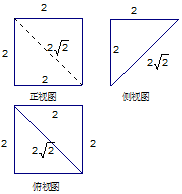

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
8.已知抛物线x2=4y的焦点为F,准线为l,抛物线的对称轴与准线交于点Q,P为抛物线上的动点,|PF|=m|PQ|,当m最小时,点P恰好在以F,Q为焦点的椭圆上,则椭圆的离心率为( )
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.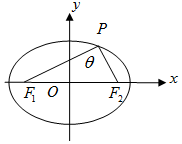 椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.
椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.