题目内容
已知集合A={x||x+1|<2},集合B={x|x2+4x≤0},则A∩B=( )
| A、[-4,0] |
| B、[-4,1) |
| C、(-3,1) |
| D、(-3,0] |
考点:交集及其运算
专题:集合
分析:分别求解绝对值的不等式和二次不等式化简集合A,B,然后直接利用交集运算求解.
解答:
解:由|x+1|<2,得-2<x+1<2,解得-3<x<1,
∴A={x||x+1|<2}={x|-3<x<1},
由x2+4x≤0,得-4≤x≤0.
∴集合B={x|x2+4x≤0}={x|-4≤x≤0},
如图,

则A∩B=(-3,0].
故选:D.
∴A={x||x+1|<2}={x|-3<x<1},
由x2+4x≤0,得-4≤x≤0.
∴集合B={x|x2+4x≤0}={x|-4≤x≤0},
如图,

则A∩B=(-3,0].
故选:D.
点评:本题考查了交集及其运算,考查了绝对值不等式和一元二次不等式的解法,是基础的计算题.

练习册系列答案
相关题目
将参加数学竞赛的600名学生编号为:001,002,…,600.采用系统抽样的方法抽取一个容量为50的样本,已知随机抽取的一个号码为003,则从编号为496到600的号码中,抽取的人数为( )
| A、7 | B、8 | C、9 | D、10 |
问题:①三种不同的容器中分别装有同一型号的零件400个、200个、150个,现在要从这750个零件中抽取一个容量为50的样本;②从20名学生中选出3名参加座谈会.
方法:Ⅰ.简单随机抽样法;Ⅱ.系统抽样法;Ⅲ.分层抽样法.其中问题与方法配对合适的是( )
方法:Ⅰ.简单随机抽样法;Ⅱ.系统抽样法;Ⅲ.分层抽样法.其中问题与方法配对合适的是( )
| A、①Ⅰ,②Ⅱ |
| B、①Ⅲ,②Ⅰ |
| C、①Ⅱ,②Ⅰ |
| D、①Ⅲ,②Ⅱ |
复数
的共轭复数是( )
| 1 |
| i |
| A、i | B、-i | C、1 | D、0 |
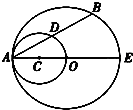 如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.
如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.