题目内容
17．设直线a与平面α相交但不垂直，则下列说法中正确的是（ ）| A． | 在平面α内没有直线与直线a垂直 | |
| B． | 在平面α内有且只有一条直线与直线a垂直 | |
| C． | 在平面α内有无数条直线与直线a垂直 | |
| D． | 在平面α内存在两条相交直线与直线a垂直 |
分析 作P作PO⊥α于O，利用线面垂直的性质定理进行判断即可．
解答 
解如图，作P作PO⊥α于O，
则AO是a在α内的射影，
若b⊥AO，
则b⊥平面PAO，
则b⊥a，
则满足b⊥AO的直线b有无数条，
即在平面α，内有无数条直线与直线a垂直，
故选：C．
点评 本题主要考查命题的真假判断，涉及线面垂直的判定和性质，属于中档题．
练习册系列答案
相关题目
7．若函数f（x）=sin（ωx+$\frac{π}{6}$）-cosωx的图象相邻两个对称中心之间的距离为$\frac{π}{2}$，则f（x）的一个单调增区间为（ ）
| A． | （-$\frac{π}{6}$，$\frac{π}{3}$） | B． | （-$\frac{π}{3}$，$\frac{π}{6}$） | C． | （$\frac{π}{6}$，$\frac{2π}{3}$） | D． | （$\frac{π}{3}$，$\frac{5π}{6}$） |
8．复数Z=$\frac{2+ai}{1+i}$（a∈R）在复平面内对应的点在虚轴上，则a=（ ）
| A． | 2 | B． | -2 | C． | 1 | D． | -1 |
12．
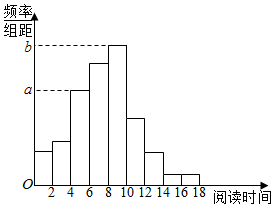从某校随机抽取200名学生，获得了他们的一周课外阅读时间（单位：小时）的数据，整理得到数据分组级频数分布直方图：
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
（2）求频率分布直方图中的a，b的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的200名学生该周课外阅读时间的平均数在第几组．
从某校随机抽取200名学生，获得了他们的一周课外阅读时间（单位：小时）的数据，整理得到数据分组级频数分布直方图：| 编号 | 分组 | 频数 |
| 1 | [0，2） | 12 |
| 2 | [2，4） | 16 |
| 3 | [4，6） | 34 |
| 4 | [6，8） | 44 |
| 5 | [8，10） | 50 |
| 6 | [10，12） | 24 |
| 7 | [12，14） | 12 |
| 8 | [14，16） | 4 |
| 9 | [16，18） | 4 |
| 合计 | 200 | |
（2）求频率分布直方图中的a，b的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的200名学生该周课外阅读时间的平均数在第几组．
2．（x+2y）7展开式中系数最大的项是（ ）
| A． | 68y7 | B． | 112x3y4 | C． | 672x2y5 | D． | 1344x2y5 |