题目内容
已知h(x)=lnx,g(x)=|h(x)|,
(1)写出g(x)的定义域,并作出y=g(x)的简图;
(2)若g(x1)=g(x2)(其中0<x1<x2),求证:x1•x2=1,x1+x2>2;
(3)判断f(x)=x-
是否存在极值?若存在,证明你的结论并求出所有极值;若不存在,说明理由.
(1)写出g(x)的定义域,并作出y=g(x)的简图;
(2)若g(x1)=g(x2)(其中0<x1<x2),求证:x1•x2=1,x1+x2>2;
(3)判断f(x)=x-
| h(x) |
| x |
考点:利用导数研究函数的极值,函数的定义域及其求法
专题:导数的综合应用
分析:(1)由函数的表达式直接写出即可,
(2)由图知0<x1<1<x2,由|lnx1|=|lnx2|⇒-lnx1=lnx2,x1+x2=x1+
>2
即x1+x2>2,从而问题得证;
(3)由题意求出函数f(x)在(0,1)递减,在(1,+∞)递增,从而求出函数f(x)有1个极小值,求出即可.
(2)由图知0<x1<1<x2,由|lnx1|=|lnx2|⇒-lnx1=lnx2,x1+x2=x1+
| 1 |
| x1 |
x1•
|
(3)由题意求出函数f(x)在(0,1)递减,在(1,+∞)递增,从而求出函数f(x)有1个极小值,求出即可.
解答:
解:(1)g(x)的定义域为(0,+∞),图象如图示:
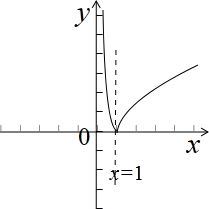 ;
;
(2)由图知0<x1<1<x2,
∴lnx1<0,lnx2>0,
∴g(x1)=g(x2)
即|lnx1|=|lnx2|⇒-lnx1=lnx2
⇒lnx1+lnx2=0⇒x1•x2=1,
∴x1+x2=x1+
>2
即x1+x2>2;
(3)∵f(x)=x-
,
∴f′(x)=
,
经观察得f′(x)=0,得x=1,
令g(x)=x2+lnx-1,则:g′(x)=2x+
,
当x>0时,g′(x)>0,即y=g(x)在(0,+∞)递增,
∴f′(x)=0有唯一的根x=1,
当x∈(0,1)时,f′(x)=
<
=0,
∴f(x)在(0,1)递减,
当x∈(1,+∞)时,f′(x)=
>
=0,
∴f(x)在(1,+∞)递增,
∴x=1是f(x)的唯一极小值点,
极小值是f(1)=1.
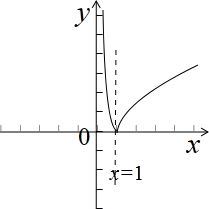 ;
;(2)由图知0<x1<1<x2,
∴lnx1<0,lnx2>0,
∴g(x1)=g(x2)
即|lnx1|=|lnx2|⇒-lnx1=lnx2
⇒lnx1+lnx2=0⇒x1•x2=1,
∴x1+x2=x1+
| 1 |
| x1 |
x1•
|
(3)∵f(x)=x-
| h(x) |
| x |
∴f′(x)=
| x2+lnx-1 |
| x2 |
经观察得f′(x)=0,得x=1,
令g(x)=x2+lnx-1,则:g′(x)=2x+
| 1 |
| x |
当x>0时,g′(x)>0,即y=g(x)在(0,+∞)递增,
∴f′(x)=0有唯一的根x=1,
当x∈(0,1)时,f′(x)=
| g(x) |
| x2 |
| g(1) |
| x2 |
∴f(x)在(0,1)递减,
当x∈(1,+∞)时,f′(x)=
| g(x) |
| x2 |
| g(1) |
| x2 |
∴f(x)在(1,+∞)递增,
∴x=1是f(x)的唯一极小值点,
极小值是f(1)=1.
点评:本题考查了函数的单调性,函数的极值问题,考查数形结合思想,等式及不等式的证明问题,本题属于综合题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知集合A={x|x-2≤1,x∈Z+},则集合A的真子集的个数为( )
| A、3个 | B、6个 | C、7个 | D、8个 |
有三个游戏规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,问其中不公平的游戏是( )
| 游戏1 | 游戏2 | 游戏3 |
| 袋中有3个黑球,1白球 | 袋中有2个黑球,2个白球 | 袋中有1黑球,1个白球 |
| 取1个球,再取1个球 | 取1个球,再取1个球 | 取1个球 |
| 若取出2个球同色,则甲胜 | 若取出2个球同色,则甲胜 | 若取出黑球,则甲胜 |
| 若取出2个球异色,则乙胜 | 若取出2个球异色,则乙胜 | 若取出白球,则乙胜 |
| A、.游戏2 | B、游戏3 |
| C、游戏1和游戏2 | D、游戏1 |
乘积5×6×7×…×20等于( )
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
若
<
<0,则下列结论不正确的是( )
| 1 |
| a |
| 1 |
| b |
| A、a2<b2 | ||||
| B、ab<b2 | ||||
| C、|a|+|b|>|a+b| | ||||
D、
|