题目内容
若log2a
<0,则a的取值范围是( )
| 1+a2 |
| 1+a |
A、(
| ||
| B、(1,+∞) | ||
C、(
| ||
D、(0,
|
分析:讨论底数与1的大小,然后根据对数的单调性建立不等关系,解之即可求出a的取值范围.
解答:解:当0<2a<1时,
>1,无解
当2a>1时,0<
<1,解得
<a<1
综上所述:
<a<1
故选C.
| 1+a2 |
| 1+a |
当2a>1时,0<
| 1+a2 |
| 1+a |
| 1 |
| 2 |
综上所述:
| 1 |
| 2 |
故选C.
点评:本题主要考查了对数函数的单调性与特殊点,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 恒成立,求实数M的最小值.
恒成立,求实数M的最小值. 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.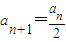 ;当an为奇数时,
;当an为奇数时,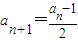 .
.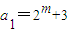 (m>3且m∈N),数列{an}的前n项和为Sn,求证:
(m>3且m∈N),数列{an}的前n项和为Sn,求证: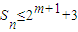 ;
;