题目内容
已知数列{an}具有性质:①a1为整数;②对于任意的正整数n,当an为偶数时,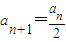 ;当an为奇数时,
;当an为奇数时,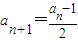 .
.(1)若a1为偶数,且a1,a2,a3成等差数列,求a1的值;
(2)设
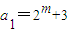 (m>3且m∈N),数列{an}的前n项和为Sn,求证:
(m>3且m∈N),数列{an}的前n项和为Sn,求证: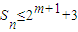 ;
;(3)若a1为正整数,求证:当n>1+log2a1(n∈N)时,都有an=0.
【答案】分析:(1)先设a1=2k,a2=k,得到a3=0,再分两种情况:k是奇数,若k是偶数,即可求出a1的值;
(2)根据题意知,当m>3时,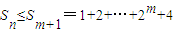 .再利用等比数列的求和公式即可证得结果;
.再利用等比数列的求和公式即可证得结果;
(3)由于n>1+log2a1,从而n-1>log2a1,得出2n-1>a1由定义可得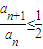 ,利用累乘的形式有
,利用累乘的形式有 ,从而
,从而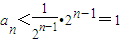 ,再根据an∈N,得出当n>1+log2a1(n∈N)时,都有an=0.
,再根据an∈N,得出当n>1+log2a1(n∈N)时,都有an=0.
解答:解:(1)设a1=2k,a2=k,则:2k+a3=2k,a3=0
分两种情况:k是奇数,则 ,k=1,a1=2,a2=1,a3=0
,k=1,a1=2,a2=1,a3=0
若k是偶数,则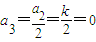 ,k=0,a1=0,a2=0,a3=0
,k=0,a1=0,a2=0,a3=0
(2)当m>3时,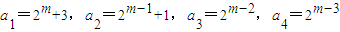 ,
,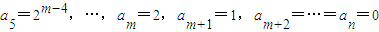
∴
(3)∵n>1+log2a1,∴n-1>log2a1,∴2n-1>a1
由定义可知:
∴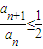
∴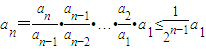
∴
∵an∈N,∴an=0,
综上可知:当n>1+log2a1(n∈N)时,都有an=0
点评:本题主要考查了等差数列与等比数列的综合,同时考查了等比数列的通项公式、等比数列前n项求和公式,解题时要认真审题,仔细观察规律,避免错误,属于中档题.
(2)根据题意知,当m>3时,
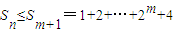 .再利用等比数列的求和公式即可证得结果;
.再利用等比数列的求和公式即可证得结果;(3)由于n>1+log2a1,从而n-1>log2a1,得出2n-1>a1由定义可得
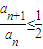 ,利用累乘的形式有
,利用累乘的形式有 ,从而
,从而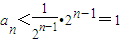 ,再根据an∈N,得出当n>1+log2a1(n∈N)时,都有an=0.
,再根据an∈N,得出当n>1+log2a1(n∈N)时,都有an=0.解答:解:(1)设a1=2k,a2=k,则:2k+a3=2k,a3=0
分两种情况:k是奇数,则
 ,k=1,a1=2,a2=1,a3=0
,k=1,a1=2,a2=1,a3=0若k是偶数,则
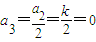 ,k=0,a1=0,a2=0,a3=0
,k=0,a1=0,a2=0,a3=0(2)当m>3时,
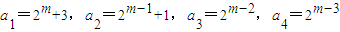 ,
,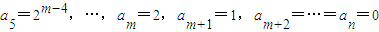
∴

(3)∵n>1+log2a1,∴n-1>log2a1,∴2n-1>a1
由定义可知:

∴
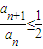
∴
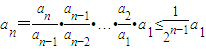
∴

∵an∈N,∴an=0,
综上可知:当n>1+log2a1(n∈N)时,都有an=0
点评:本题主要考查了等差数列与等比数列的综合,同时考查了等比数列的通项公式、等比数列前n项求和公式,解题时要认真审题,仔细观察规律,避免错误,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
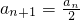 ;当an为奇数时,
;当an为奇数时,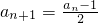 .
.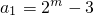 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: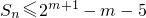 .
.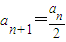 ;当an为奇数时,
;当an为奇数时,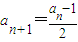 .
.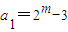 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: .( )
.( )