题目内容
13.函数y=-2cosx-3,当x的取值集合为{x|x=2kπ+π,k∈Z}时,y取得最大值;当x的取值集合为{x|x=2kπ,k∈Z}时,y取得最小值-5.分析 由条件利用余弦函数的定义域和值域,得出结论.
解答 解:对于函数y=-2cosx-3,
当x=2kπ+π,k∈Z时,y取得最大值-1,
故当x的取值集合为{x|x=2kπ+π,k∈Z}时,y取得最大值.
当x=2kπ,k∈Z时,y取得最小值为-5,
当x的取值集合为{x|x=2kπ,k∈Z} 时,y取得最小值.
故答案为:{x|x=2kπ+π,k∈Z};{x|x=2kπ,k∈Z};-5.
点评 本题主要考查余弦函数的最值、余弦函数的定义域和值域,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
1.设数列{an}满足${a_n}={i^n}$,i是虚数单位,n∈N*,则数列{an}的前2015项和为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
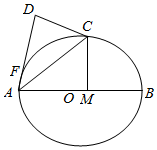 如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.
如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.