题目内容
16.关于平面向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$,有下列三个命题:①若$\overrightarrow{a}$∥$\overrightarrow{b}$且$\overrightarrow{a}$∥$\overrightarrow{c}$,则$\overrightarrow{b}$∥$\overrightarrow{c}$;
②若$\overrightarrow{a}$=(2,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=-6;
③非零向量$\overrightarrow{a}$和$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为30°.
其中正确命题的序号为②③(写出所有真命题的序号).
分析 ①当$\overrightarrow{a}$=$\overrightarrow{0}$时,$\overrightarrow{b}$∥$\overrightarrow{c}$不一定成立;
②利用向量平行的坐标表示,列出方程求出k的值;
③利用平面向量的几何意义,画出图形,即可得出正确的结论.
解答 解:对于①,当$\overrightarrow{a}$∥$\overrightarrow{b}$且$\overrightarrow{a}$∥$\overrightarrow{c}$,若$\overrightarrow{a}$=$\overrightarrow{0}$,则$\overrightarrow{b}$∥$\overrightarrow{c}$不一定成立,∴①错误;
对于②,当$\overrightarrow{a}$=(2,k),$\overrightarrow{b}$=(-2,6),且$\overrightarrow{a}$∥$\overrightarrow{b}$时,-2k-2×6=0,解得k=-6,∴②正确;
对于③,根据平面向量的几何意义,得;
非零向量$\overrightarrow{a}$和$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|时,以|$\overrightarrow{a}$|、|$\overrightarrow{b}$|、|$\overrightarrow{a}$-$\overrightarrow{b}$|为三边的三角形是等腰三角形,
如图所示,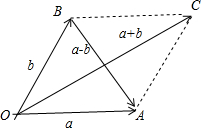
则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为30°,∴③正确.
综上,正确的命题是②③.
故答案为:②③.
点评 本题考查了平面向量的基本概念的应用问题,也考查了平面向量的几何意义的应用问题,是基础题目.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | x1+x2+x3有最小值,x1x2x3无最大值 | |
| B. | x1+x2+x3无最小值,x1x2x3有最大值 | |
| C. | x1+x2+x3有最小值,x1x2x3有最大值 | |
| D. | x1+x2+x3无最小值,x1x2x3无最大值 |
| A. | M⊆N | B. | M=N | C. | N⊆M | D. | M∩N=∅ |