题目内容
11.已知α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{5}}{5}$,$\overrightarrow{a}$=(cosα,sinα),$\overrightarrow{b}$=(cos2α,sin2α).求:(1)判断$\overrightarrow{a}$与$\overrightarrow{b}$是否平行?
(2)求$\overrightarrow{a}$$•\overrightarrow{b}$的值.
分析 (1)利用向量共线定理即可判断出.
(2)由α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{5}}{5}$,可得cosα=-$\sqrt{1-si{n}^{2}α}$.利用数量积运算性质可得$\overrightarrow{a}•\overrightarrow{b}$=cosα,即可得出.
解答 解:(1)∵cos2αsinα-cosαsin2α=-sinα=-$\frac{\sqrt{5}}{5}$≠0,因此$\overrightarrow{a}$与$\overrightarrow{b}$不平行.
(2)∵α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{5}}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{2\sqrt{5}}{5}$.
∴$\overrightarrow{a}•\overrightarrow{b}$=cosαcos2α+sinαsin2α=cosα=-$\frac{2\sqrt{5}}{5}$.
点评 本题考查了向量共线定理、数量积运算性质、同角三角函数基本关系式,考查了推理能力 与计算能力,属于中档题.

练习册系列答案
相关题目
1.为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
3.不等式x(x-1)≥x的解集为( )
| A. | {x|x≤0或x≥2} | B. | {x|0≤x≤2} | C. | {x|x≥2} | D. | {x|x≤0或x≥1} |
1.将函数y=sinx的图象向左平移$\frac{π}{12}$个单位,然后将图象所有点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),则所得函数解析式为( )
| A. | $y=sin(\frac{1}{2}x+\frac{π}{12})$ | B. | $y=sin(\frac{1}{2}x-\frac{π}{12})$ | C. | $y=sin(2x+\frac{π}{12})$ | D. | $y=sin(2x-\frac{π}{6})$ |
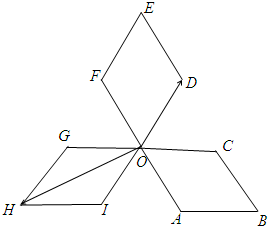 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( ) 如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.
如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.