题目内容
7.定义min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,若关于x的方程$min\left\{{2\sqrt{x},|{x-2}|}\right\}=m$(m∈R)有三个不同的实根x1,x2,x3,则( )| A. | x1+x2+x3有最小值,x1x2x3无最大值 | |
| B. | x1+x2+x3无最小值,x1x2x3有最大值 | |
| C. | x1+x2+x3有最小值,x1x2x3有最大值 | |
| D. | x1+x2+x3无最小值,x1x2x3无最大值 |
分析 先比较2$\sqrt{x}$与|x-2|的大小以确定f(x)的解析式,然后结合函数的图象即可判断符合条件的m的范围,求出x1,x2,x3,的值,从而求出x1+x2+x3的取值范围和x1•x2•x3的最值.
解答 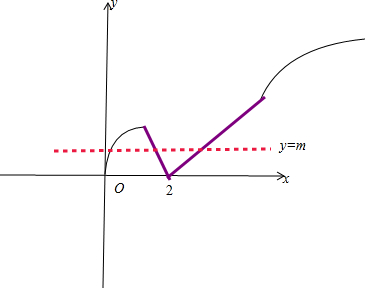 解:令y=f(x)=min{2$\sqrt{x}$,|x-2|},
解:令y=f(x)=min{2$\sqrt{x}$,|x-2|},
由2$\sqrt{x}$≥|x-2|可得x2-8x+4≤0,
解可得4-2$\sqrt{2}$≤x≤4+2$\sqrt{2}$,
当4-2$\sqrt{2}$≤x≤4+2$\sqrt{2}$时,
2$\sqrt{x}$≥|x-2|,此时f(x)=|x-2|;
当x>4+2$\sqrt{2}$或0≤x<4-3$\sqrt{2}$时,
2$\sqrt{2}$<|x-2|,此时f(x)=2$\sqrt{x}$,
其图象如图所示,
∵f(4-2$\sqrt{2}$)=2$\sqrt{2}$-2,
由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:
0<m<2$\sqrt{3}$-2,
不妨设0<x1<x2<2<x3,
则由2$\sqrt{{x}_{1}}$=m得x1=$\frac{{m}^{2}}{4}$,
由|x2-2|=2-x2=m,得x2=2-m,
由|x3-2|=x3-2=m,得x3=m+2,
∴x1+x2+x3=$\frac{{m}^{2}}{4}$+2-m+m+2=$\frac{{m}^{2}}{4}$+4,
当m=0时,$\frac{{m}^{2}}{4}$+4=4,m=2$\sqrt{3}$-2时,$\frac{{m}^{2}}{4}$+4=8-2$\sqrt{3}$,
∴4<x1+x2+x3<8-2$\sqrt{3}$.
即x1+x2+x3无最小值;
x1•x2•x3=$\frac{{m}^{2}}{4}$(2-m)(m+2)=$\frac{1}{4}$m2(4-m2)≤$\frac{1}{4}$•($\frac{{m}^{2}+4-{m}^{2}}{2}$)2=1,
当且仅当m=$\sqrt{2}$∈(0,2$\sqrt{3}$-2),则x1•x2•x3取得最大值1.
故选:B.
点评 本题以新定义为载体,主要考查了函数的交点个数的判断,解题的关键是结合函数的图象.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| 分组 | 频数 | 频率 |
| 50~70 | 30 | 0.06 |
| 70~90 | 0.42 | |
| 90~110 | 190 | |
| 110~130 | 60 | 0.12 |
| 130~150 | ||
| 合计 | 500 | 1.00 |
(2)估计该市文科调研测试的平均分数(同一组中的数据用该区间的中点值作代表);
(3)用分层抽样的方法在分数段[50,70),[130,150)的学生中抽取一个容量为4的样本,将该样本看成一个总体,从中任取2人,求2人都在分数段[50,70)的概率.
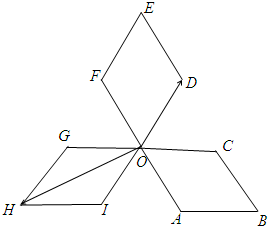 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )