题目内容
15. 如图,某流动海洋观测船开始位于灯塔B的北偏东θ(0<θ<$\frac{π}{2}$)方向,且满足2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投浮标,使得C点于A点的距离为4$\sqrt{3}$km,则该观测船行驶的最远航程为8km.
如图,某流动海洋观测船开始位于灯塔B的北偏东θ(0<θ<$\frac{π}{2}$)方向,且满足2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投浮标,使得C点于A点的距离为4$\sqrt{3}$km,则该观测船行驶的最远航程为8km.
分析 利用条件2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,0<θ<$\frac{π}{2}$,求出θ,得出AD+DC=BC,求该观测船行驶的最远航程,即求BC的最大值,当且仅当BC为△ABC的外接圆的直径时,取得最大值,由正弦定理可得结论.
解答 解:∵2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,
∴2sin2($\frac{π}{4}$+θ)-1=$\sqrt{3}$cos2θ,
∴-cos($\frac{π}{2}$+2θ)=$\sqrt{3}$cos2θ,
∴sin2θ-$\sqrt{3}$cos2θ=0
∴2sin(2θ-$\frac{π}{3}$)=0,
∵0<θ<$\frac{π}{2}$,
∴θ=$\frac{π}{6}$,
∴∠ABC=$\frac{π}{3}$,
∵AB=AD,∴AB=AD=BD,
∴AD+DC=BC,
求该观测船行驶的最远航程,即求BC的最大值,当且仅当BC为△ABC的外接圆的直径时,取得最大值,
由正弦定理可得2R=$\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$=8.
故答案为:8.
点评 本题考查三角函数公式的运用,考查正弦定理,解题时,求该观测船行驶的最远航程,转化为求BC的最大值,当且仅当BC为△ABC的外接圆的直径时,取得最大值是关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
3.已知m,n是两条不同的直线,α,β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
| A. | α⊥β且m⊆α | B. | m⊥n且n⊆β | C. | α⊥β且m∥α | D. | m⊥n且n∥β |
20.平面α与平面β平行的条件可以是( )
| A. | α内有无数条直线都与β平行 | |
| B. | 直线a?α,直线b?β,且a∥β,b∥α | |
| C. | α内的任何直线都与β平行 | |
| D. | 直线a∥α,a∥β,且直线a不在α内,也不在β内 |
5.连锁水果店店主每天以每件50元购进水果若干件,以80元一件销售;若供大于求,当天剩余水果以40元一件全部退回;若供不应求,则立即从连锁店60元一件调剂,以80元一件销售.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
若水果店一天购进5件水果,以30天记录的各需求量发生的频率作为概率,求每天的利润在区间[150,200]的概率.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.
如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.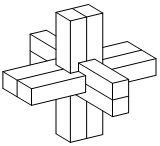 鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )
鲁班锁,是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下,左右,前后完全对称,从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为( )