题目内容
用 ,
, ,
, 表示空间中三条不同的直线,
表示空间中三条不同的直线,  表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若 ,
,  , 则
, 则 ∥
∥ ; ② 若
; ② 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ;
;
③ 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ; ④ 若
; ④ 若

 ,
, 

 , 则
, 则 ∥
∥ .
.
其中真命题的序号是( )
A.① ② B.② ③ C.① ④ D.② ④
D
【解析】
试题分析:若 ,
,  , 则
, 则 ∥
∥ 或
或 与
与 相交或
相交或 与
与 异面,所以①是假命题;平行于同一直线的两条直线平行,所以②是真命题;若
异面,所以①是假命题;平行于同一直线的两条直线平行,所以②是真命题;若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ 或
或 与
与 相交或
相交或 与
与 异面,所以③是假命题;若两条直线垂直于同一个平面,则这两条直线平行,所以④是真命题.故选D.
异面,所以③是假命题;若两条直线垂直于同一个平面,则这两条直线平行,所以④是真命题.故选D.
考点:空间点、线、面的位置关系.

练习册系列答案
相关题目
(本题12分) 某县教研室要分析学生初中升学的数学成绩对高一年级数学成绩有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末成绩y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)计算入学成绩 与高一期末成绩
与高一期末成绩 的相关系数;
的相关系数;
(2)对变量 与
与 进行相关性检验,如果
进行相关性检验,如果 与
与 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
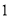 的正三角形
的正三角形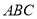 的边
的边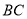 上有
上有 (
(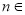 N*,
N*,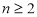 )等分点,
)等分点, 的方向依次为
的方向依次为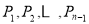 ,记
,记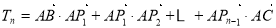 ,
,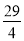 ②
②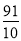 ③
③ ④
④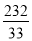 ,则
,则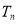 的值不可能的共有( )
的值不可能的共有( )

 ,公比不等于
,公比不等于 的等比数列
的等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列. 的通项公式;
的通项公式; ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
 .
. 中,设不等式组
中,设不等式组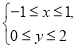 所表示的平面区域是
所表示的平面区域是 ,从区域
,从区域 中随机取点
中随机取点 ,则
,则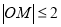 的概率是 .
的概率是 . ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
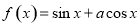
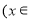 R
R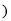 ,
,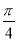 是函数
是函数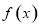 的一个零点.
的一个零点.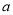 的值,并求函数
的值,并求函数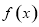 的单调递增区间;
的单调递增区间;
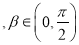 ,且
,且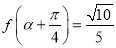 ,
,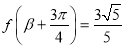 ,求
,求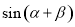 的值.
的值. ,经过
,经过 天后体积与天数
天后体积与天数 的关系式为:
的关系式为: ,若新丸经过50天后,体积变为
,若新丸经过50天后,体积变为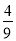
 ;若一个新丸体积变为
;若一个新丸体积变为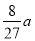 ,则需经过的天数为
,则需经过的天数为