题目内容

复数范围内因式分解x2+4x+5=
 
．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：根据在复数范围内解实系数的一元二次方程的方法，求得 x2+4x+5=0的两个根，即可对 x2+4x+5进行因式分解．
解答： 解：由于判别式△=16-20=-4＜0，∴x2+4x+5=0的两个根为
-4±
4
i
2
=-2±i，
∴x2+4x+5=[x-（-2+i）][x-（-2-i）]，
故答案为：[x-（-2+i）][x-（-2-i）]．
点评：本题主要考查在复数范围内解实系数的一元二次方程的方法，属于基础题．
练习册系列答案
相关题目
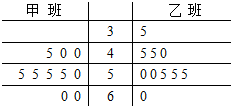某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩（满分60分），统计后获得成绩数据的茎叶图（以十位数字为茎，个位数字为叶），如图所示：
（Ⅰ）分别计算两组数据的平均数，并比较哪个班级的客观题平均成绩更好；
（Ⅱ）从这两组数据各取两个数据，求其中至少有2个满分（60分）的概率；
（Ⅲ）规定客观题成绩不低于55分为“优秀客观卷”，以这20人的样本数据来估计此次高三数学模拟的总体数据，若从总体中任选4人，记X表示抽到“优秀客观卷”的学生人数，求X的分布列及数学期望．
在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线ρsin（θ+
π
3
）=
1
2
与曲线
x=
1
2
(t+
1
t
)
y=t-
1
t
（t为参数）相交于A，B两点，若M为线段AB的中点，则直线OM的斜率为
 
．
等比数列{an}的各项均为正数，a2=8，且2a4，a3，4a5成等差数列，则{an}的前5项和为
 
．
若（1+2x）2014=a0+a1x+…+a2014x2014（x∈R），则
a1
2
-
a2
22
+
a3
23
-
a4
24
+…-
a2014
22014
的值为
 
．
已知复数z满足（z-2）i=1+i（i是虚数单位），则|z|=
 
．
已知圆C的半径为3，直径AB上一点D使
AB
=3
AD
，E，F为另一直径的两个端点，则
DE
•
DF
=
 
．
在直角坐标系中，定义两点P（x1，y1）、Q（x2、y2）之间的“直角距离”为d（P，Q）=|x1-x2|+|y1-y2|，现有下列四个命题：
①已知两点P（2，3），Q（sin2α，cos2α）（α∈R），则d（P，Q）为定值；
②原点O到直线x-y+1=0上任一点P的直角距离d（O，P）的最小值为
2
2
；
③若|PQ|表示P、Q两点间的距离，那么|PQ|≥
2
2
d（P，Q）；
④设点A（x，y）且x，y∈Z，若点A在过P（0，2）与Q（5，7）的直线上，且点A到点P与Q的直角距离之和等于10，那么满足条件的点A只有5个．
其中是真命题的是
 
（写出所有真命题的序号）．
在平面直角坐标系中，定义d（P，Q）=|x1-x2|+|y1-y2|为P（x1，y1），Q（x2，y2）两点之间的“折线距离”．在这个定义下，给出下列命题：
①到原点的“折线距离”等于1的点的集合是一个正方形；
②到原点的“折线距离”等于1的点的集合是一个圆；
③到点P（-1，0），Q（1，0）两点的“折线距离”相等的点的轨迹方程是x=0；
④到点P（-1，0），Q（1，0）两点的“折线距离”的差的绝对值为1的点的集合是两条平行线．
其中正确结论的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网