题目内容
已知椭圆C的离心率为
,椭圆C的右焦点F2和抛物线y2=4
x的焦点重合,椭圆C与y轴的一个交点为N,且F1是椭圆C的左焦点.
(1)求证:△NF1F2是等腰直角三角形;
(2)当过点P(4,1)的动直线l与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足
=
,求点Q的轨迹方程.
| ||
| 2 |
| 2 |
(1)求证:△NF1F2是等腰直角三角形;
(2)当过点P(4,1)的动直线l与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足
|
| ||
|
|
|
| ||
|
|
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意解得a2=4,b2=2,所求椭圆方程为
+
=1.由此能证明△NF1F2是等腰直角三角形.
(Ⅱ)设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).由题可设λ=
=
,则λ>0且λ≠1.由此利用A,P,B,Q四点共线,结合已知条件能推导出点Q的轨迹是直线在椭圆内的部分,方程为2x+y-2=0.
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).由题可设λ=
|
| ||
|
|
|
| ||
|
|
解答:
(Ⅰ)证明:由题意解得a2=4,b2=2,
所求椭圆方程为
+
=1.
∴F1(-
,0),F2(
,0),
∵椭圆C与y轴的一个交点为N,
∴△NF1F2是等腰直角三角形.(3分)
(Ⅱ)解:设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题可设λ=
=
,则λ>0且λ≠1.
又A,P,B,Q四点共线,从而
=-λ
,
=λ
.
于是4=
,1=
x=
,y=
,(5分)
从而
=4x,…(1)
=y,…(2)
又点A、B在椭圆C上,即
+2
=4,…(3),
+2
=4,…(4)
(1)+(2)×2并结合(3),(4)得4x+2y=4,
即点Q的轨迹是直线在椭圆内的部分,方程为2x+y-2=0.(10分)
所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 2 |
∴F1(-
| 2 |
| 2 |
∵椭圆C与y轴的一个交点为N,
∴△NF1F2是等腰直角三角形.(3分)
(Ⅱ)解:设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题可设λ=
|
| ||
|
|
|
| ||
|
|
又A,P,B,Q四点共线,从而
| AP |
| PB |
| AQ |
| QB |
于是4=
| x1-λx2 |
| 1-λ |
| y1-λy2 |
| 1-λ |
| x1+λx2 |
| 1+λ |
| y1+λy2 |
| 1+λ |
从而
| ||||
| 1-λ2 |
| ||||
| 1-λ2 |
又点A、B在椭圆C上,即
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
(1)+(2)×2并结合(3),(4)得4x+2y=4,
即点Q的轨迹是直线在椭圆内的部分,方程为2x+y-2=0.(10分)
点评:本题考查三角形为等腰直角三角形的证明,考查点的轨迹方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相交,则双曲线的离心率的取值范围是( )
| y2 |
| a2 |
| x2 |
| b2 |
| A、(1,2) | ||||
B、(
| ||||
C、(1,
| ||||
| D、(2,+∞) |
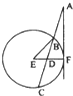 如图,过圆E外一点A作一条直线与圆E交与B,且AB=
如图,过圆E外一点A作一条直线与圆E交与B,且AB=