Question

已知函数f（x）=|a-

b

x

|，a＞0，b＞0，x≠0，且满足：函数y=f（x）的图象与直线y=1有且只有一个交点．
（1）求实数a的值；
（2）若关于x的不等式f（x）＜4^x-1的解集为(

1

2

，+∞)，求实数b的值；
（3）在（2）成立的条件下，是否存在m，n∈R，m＜n，使得f（x）的定义域和值域均为[m，n]，若存在，求出m，n的值，若不存在，请说明理由．

Answer 1

考点：带绝对值的函数,特称命题

专题：综合题,函数的性质及应用

分析：（1）依题意，a-

b

x

=-1时方程必有一根

b

a+1

，而a-

b

x

=1无解，从而可求得a；
（2）由f（x）=|a-

1

x

|与y=4^x-1的图象知两图象的交点横坐标为

1

2

，从而可求得b；
（3）f（x）=|1-

1

x

|≥0，故必须满足n＞m＞0，f（1）=0，值域[m，n]中不包括0，定义域[m，n]中不包括1，只需讨论：当0＜m＜n＜1与1＜m＜n时，由f（x）在[m，n]上的单调性即可求得答案．

解答： 解：（1）a-

b

x

=1或a-

b

x

=-1，因为a＞0，b＞0，所以a-

b

x

=-1时方程必有一根

b

a+1

，
因此a-

b

x

=1无解，a=1…4分
（2）由f（x）=|a-

b

x

|与y=4^x-1的图象知两图象的交点横坐标为

1

2

，

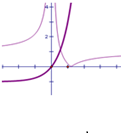
代入y=4^x-1，得交点为（

1

2

，1）代入f（x）=|a-

b

x

|知b=1…9分．
（3）∵f（x）=|1-

1

x

|≥0，故必须满足n＞m＞0，
又f（1）=0，值域[m，n]中不包括0，所以定义域[m，n]中不包括1，只需讨论：
当0＜m＜n＜1时，f（x）=

1

x

-1在[m，n]上递减，作差得：

1

m

-

1

n

=n-m，mn=1不成立；
当1＜m＜n时，f（x）=1-

1

x

在[m，n]上递增，1-

1

m

=m，1-

1

n

=n，
作差得：

1

n

-

1

m

=m-n，mn=1，不成立．
综上，不存在m，n∈R，m＜n满意…14分

点评：本题考查带绝对值的函数，着重考查数形结合思想与分类讨论思想的综合运用，考查创新能力与抽象思维能力，属于难题．