题目内容
14．在锐角△ABC中，角A、B所对的边长分别为a、b，若2asinB=$\sqrt{3}$b，则角A等于60°．分析 已知等式利用正弦定理化简，根据sinB不为0求出sinA的值，再由A为锐角，利用特殊角的三角函数值即可求出A的度数．
解答 解：利用正弦定理化简已知等式得：2sinAsinB=$\sqrt{3}$sinB，
∵sinB≠0，
∴sinA=$\frac{\sqrt{3}}{2}$，
∵A为锐角，
∴A=60°．
故答案为：60°．
点评 此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键，属于基础题．
练习册系列答案
相关题目
4．从长度分别位2、4、6、8、10的五条线段中，任取3条，则所得的3条线段中能组成三角形的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{10}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{10}$ |
2．$\root{4}{a-2}$+（a-4）0有意义，则a的取值范围是（ ）
| A． | a≥2 | B． | 2≤a＜4或a＞4 | C． | a≠2 | D． | a≠4 |
9．已知等差数列{an}的前n项和为Sn，a2=-2，S4=-4，若Sn取得最小值，则n的值为（ ）
| A． | n=2 | B． | n=3 | C． | n=2或n=3 | D． | n=4 |
19．若函数f（x）=$\left\{\begin{array}{l}{1-{2}^{x}，x≤0}\\{{x}^{3}-3x+a，x＞0}\end{array}\right.$的值域为[0，+∞），则实数a的取值范围是（ ）
| A． | 2≤a≤3 | B． | a＞2 | C． | a≥2 | D． | 2≤a＜3 |
6．若z=$\frac{1}{1-i}$-i，则|z|=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | -$\frac{1}{2}$+$\frac{1}{2}i$ | D． | $\frac{1}{2}$+$\frac{1}{2}i$ |
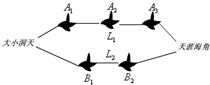（理）“十一黄金周”期间三亚景区迎来了游客高峰期．游客小李从“大小洞天”到景区“天涯海角”景区有L1，L2两条路线（如图），路线L1上有A1，A2，A3三个风景点，各风景点遇到堵塞的概率均为$\frac{2}{3}$；L2路线上有B1，B2两个风景点，各风景点遇到堵塞的概率依次为$\frac{3}{4}$，$\frac{3}{5}$．