题目内容
sin17°cos28°+sin73°cos62° ．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：原式第二项变形后，利用两角和与差的正弦函数公式化简，再利用特殊角的三角函数值计算即可．
解答：
解：原式=sin17°cos28°+cos17°sin28°=sin（17°+28°）=sin45°=
，
故答案为：
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：此题考查了两角和与差的正弦函数公式，诱导公式的作用，以及特殊角的三角函数值，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
若向量
与
不共线，
•
≠0，且
=
-
，则向量
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| c |
| a |
(
| ||||||
|
| a |
| c |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
如果向量
=（2，1），
=（-3，4），那么向量3
+4
的坐标是（ ）
| a |
| b |
| a |
| b |
| A、（19，-6） |
| B、（-6，19） |
| C、（-1，16） |
| D、（16，-1） |
已知x，y均为正数，且x≠y，则下列四个数中最小的一个是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图所示，在正方体ABCD-A1B1C1D1中，直线B1D1与平面BDC1的位置关系是（ ）
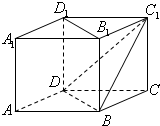
| A、平行 |
| B、垂直 |
| C、相交但不垂直 |
| D、直线B1D1在平面BDC1内 |
a，b是正数，则
，
，
三个数的大小顺序是（ ）
| a+b |
| 2 |
| ab |
| 2ab |
| a+b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知a、b、c都是实数，则“ac2＞bc2”是“a＞b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |