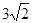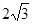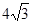题目内容
已知曲线 -
-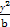 =1(ab≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且
=1(ab≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且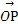 ·
·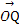 =0(O为原点),则
=0(O为原点),则 -
- 的值为 .
的值为 .
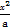 -
-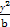 =1(ab≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且
=1(ab≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且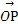 ·
·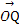 =0(O为原点),则
=0(O为原点),则 -
- 的值为 .
的值为 .2
将y=1-x代入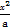 -
-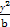 =1,得
=1,得
(b-a)x2+2ax-(a+ab)=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=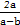 ,x1x2=
,x1x2=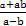 .
.
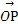 ·
·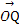 =x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1.所以
=x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1.所以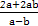 -
-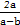 +1=0,
+1=0,
即2a+2ab-2a+a-b=0,
即b-a=2ab,所以 -
- =2.
=2.
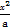 -
-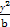 =1,得
=1,得(b-a)x2+2ax-(a+ab)=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=
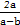 ,x1x2=
,x1x2=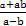 .
.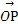 ·
·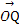 =x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1.所以
=x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1.所以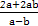 -
-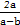 +1=0,
+1=0,即2a+2ab-2a+a-b=0,
即b-a=2ab,所以
 -
- =2.
=2.
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
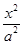 -
-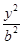 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=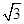 x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 .
x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 .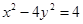 有共同的渐近线,并且经过点
有共同的渐近线,并且经过点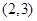 的双曲线是 。
的双曲线是 。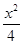 -
-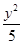 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|= |AF|,则A点的横坐标为( )
|AF|,则A点的横坐标为( )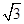
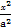 -
-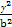 =1(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线x=
=1(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线x=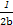 y2的焦点分成3∶2的两段,则此双曲线的离心率为( )
y2的焦点分成3∶2的两段,则此双曲线的离心率为( )
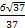
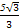
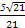


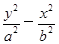 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为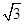 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )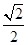 x
x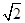 x
x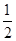 x
x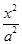 -
-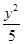 =1的右焦点为(3,0),则该双曲线的离心率等于( )
=1的右焦点为(3,0),则该双曲线的离心率等于( )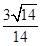
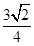
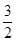
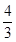
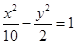 的焦距为
的焦距为