题目内容
11.证明:如果a,b,c是△ABC的三个内角A,B,C所对的边,且a(1-2cosA)+b(1-2cosB)+c(1-2cosC)=0,那么△ABC是等边三角形.分析 通过余弦定理将角的余弦值用三边表示出来,代入a(1-2cosA)+b(1-2cosB)+c(1-2cosC)=0,化简、配方计算即得结论.
解答 证明:由余弦定理可知cosA=$\frac{1}{2bc}$(b2+c2-a2),cosB=$\frac{1}{2ac}$(a2+c2-b2),cosC=$\frac{1}{2ab}$(a2+b2-c2),
又∵a(1-2cosA)+b(1-2cosB)+c(1-2cosC)=0,
∴a[1-2•$\frac{1}{2bc}$(b2+c2-a2)]+b[1-2•$\frac{1}{2ac}$(a2+c2-b2)]+c[1-2•$\frac{1}{2ab}$(a2+b2-c2)]=0,
两边同乘以abc,整理得:abc(a+b+c)+a4+b4+c4-2a2b2-2b2c2-2c2a2=0,
变形得:[(a+b)2-c2](a-b)2+[(a+c)2-b2](a-c)2+[(b+c)2-a2](b-c)2=0,
由a、b、c满足三边关系可知a-b=a-c=b-c=0,即a=b=c,
即三角形为等边三角形.
点评 本题考查等边三角形的证明,利用余弦定理是解决本题的关键,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20.函数f(x)是R上的偶函数,且在[0,+∞)上单调递增,则下列各式成立的是( )
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
1.执行下列程序,则输出的S的值是( )


| A. | $-1-\frac{{\sqrt{2}}}{2}$ | B. | -1 | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
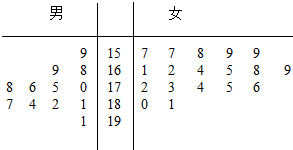 第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.