题目内容

20．函数f（x）是R上的偶函数，且在[0，+∞）上单调递增，则下列各式成立的是（　　）
A．f（-2）＞f（0）＞f（1）B．f（-2）＞f（1）＞f（0）C．f（1）＞f（0）＞f（-2）D．f（1）＞f（-2）＞f（0）

分析 利用函数f（x）是R上的偶函数，且在[0，+∞）上单调递增，即可比较大小．

解答 解：∵f（x）是R上的偶函数，∴f（-2）=f（2），
又∵f（x）在[0，+∞）上递增，
∴f（-2）＞f（1）＞f（0）．
故选：B．

点评 本题主要考查大小比较，根据函数奇偶性和单调性之间的关系是解决本题的关键．

练习册系列答案
相关题目
20．已知z=a+bi（a，b∈R），|z-$\overline{z}$|等于什么？并用图表示这一结果．
11．证明：如果a，b，c是△ABC的三个内角A，B，C所对的边，且a（1-2cosA）+b（1-2cosB）+c（1-2cosC）=0，那么△ABC是等边三角形．
8．将长度为a的木条折成三段，求三段能构成三角形的概率$\frac{1}{4}$．
15．已知正项数列{an}的首项a1=2，点P（an+1，an）在曲线x2-y2=1上．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{1}{{{a_{n+1}}+{a_n}}}$，{bn}的前n项和为Tn，证明：Tn＞-2．
5．执行如图所示的程序框图，则输出k的值为（　　）
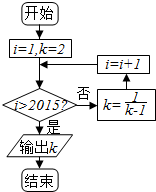
A．-1B．-2C．$\frac{1}{2}$D．2
12．阅读如图所示的程序框图，若输入i=5，则输出的k值为（　　）
A．2B．3C．4D．5
9．某网站用“10分制”调查一社区人们的幸福度．现从调查人群中随机抽取16名，如图茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：

若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．
（1）从这16人中随机选取3人，记X表示抽到“极幸福”的人数，求X的分布列及数学期望，并求出至多有1人是“极幸福”的概率；
（2）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的数学期望．
10．不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2＞0①}\\{2{x}^{2}+（5+2a）x+5a＜0②}\end{array}\right.$解集中的整数有且只有-2，则a的范围（　　）
A．[-2，2]B．[-2，2）C．[-3，2]D．[-3，2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网